Nu veți fi testați la definiții. Nici măcar nu veți întâlni aceste cuvinte în problemele de examen. Dar veți avea la examen probleme despre sarcini din viața de zi cu zi, descrise în cuvinte de zi cu zi, și va trebui să recunoașteți noțiunea / noțiunile la care face referire enunțul, pentru a identifica noțuni definite aici, și, astfel, secțiunea din celelalte capitol care e relevantă pentru rezolvarea problemei.

Populație și eșantion

Populația (numită clasic colectivitate) este o mulțime ale cărei elemente sunt în parte asemănătoare. De exemplu, populația României cuprinde ca elemente oameni din România, care au în comun specia și locul de reședință. Ca în orice mulțime, elementele ar trebui să nu se repete și ar trebui să difere în alte aspecte. Termenul s-a asociat cu demografia, dar orice mulțime de elemente asemănătoare e o populație pentru statistician.

Colectivitățile reale sunt finite, deși relațiile matematice care le discută sunt frecvent concepute în ideea că populația studiată e infinită.

Observarea totală este înregistrarea unor date despre fiecare element al populației, fără omisiuni. Exemplu tipic este recensământul.

Populațiile reale sunt dinamice (schimbătoare). De regulă, observarea totală este ori costisitoare, ori pur și simplu nu poate fi făcută în timp util. Nici un buget nu va fi suficient pentru recensământul peștilor din Marea Neagră într-un interval de timp suficient de scurt pentru ca populația să nu se fi schimbat mult. De aceea, se practică observarea parțială, adică înregistrarea datelor despre o submulțime a populației.

Eșantionul (clasic numit selecție, sample în engleză) este o submulțime dintr-o populație, aleasă în vederea observării parțiale. Procedeul de alegere al unui eșantion se numește eșantionare (eng. sampling). Chiar și cu o populație mică, numărul de eșantioane distincte este enorm. Gândiți-vă câte submulțimi de 5, 6, 7 … studenți se pot alege dintr-o grupă de doar 25. Dar, de regulă, statisticianul are acces la un singur eșantion.

O mare parte din munca statisticienilor o constituie trecerea de la informațiile detaliate ce pot fi colectate de la un eșantion la informații plauzibile despre populații și chiar indivizi necontactați din acea populație. Procesul de elaborare al acestor afirmații despre populație, pe baza informațiilor din eșantion, se numește inferență. De asemenea, rezultatul procesului de inferență se numește tot inferență, în două forme

• varianta propoziției complete (“pe baza informațiilor din eșantion, media populației este cel mai probabil 8”, sau, mai frecvent, “intervalul de încredere 95% pentru media populației este între 7 și 9”)
• varianta incompletă (“inferența dorită la finalul acestui studiu este media populației”).

Observațiile din fizică, chimie etc duc, de regulă, la ceea ce numim legi. Până azi, omenirea nu a întâlnit situații în care un corp să iasă spontan din repaus, ceea ce face prima lege a lui Newton o certitudine. Avem foarte puține îndoieli, și acelea mai mult de natură filozofică., despre viitorul unui corp în repaus. Prin contrast, inferența statistică generează legități (law-like relationships, sau statistical regularity). De exemplu, ceea ce numim legea cererii și ofertei este de fapt o legitate, pentru că, de regulă, dar nu întotdeauna, la creșterea ofertei scade preșul etc. Prin urmare, produsul inferenței statistice nu va fi o frază cu termeni preciși, și va include frecvent termeni probabilistici (“creșterea ofertei va duce cel mai probabil la scăderea prețului”).

Un alt contrast între statistică și științele naturii sau sociale este relația lor cu cauzalitatea. De exemplu, și economistul, și statisticianul pot nota tendința ratei inflației de a scădea în perioadele de șomaj crescut. Însă economiștii sunt preocupați să decidă dacă modificările în inflație cauzează modificări în șomaj sau invers. Statisticienii vor fi în primul rând interesați în a elabora ecuația sau ecuațiile ce previzionează cel mai bine, în limitele cunoașterii umane, atât rata șomajului, cât și inflația.

Elementele unei populații se numesc unități statistice. Atunci când vorbim de eșantion pot exista neclarități. De exemplu, multe sondaje sociologice se inițiază prin tragerea la sorți a unor adrese, dar chestionarele vor fi aplicate unei singure persoane de la acea adresă. Deși măsurăm (“observăm”) opiniile persoanelor, eșantionăm gospodării. Spunem că fiecare respondent este o unitate de observare, iar fiecare gospodărie este o unitate de eșantionare. Uneori faptul că gospodăria este formată din mai multe persoane este subliniat prin

• descrierea persoanei ca unitate statistică simplă
• descrierea gospodăriei ca unitate statistică complexă.

Mulțimile de unități statistice pot fi descrise în două moduri, la fel ca orice mulțime

• sintetic (engl. extensional) prin enumerarea unităților statistice, de exemplu, {0, 1, 2}, sau {George, Robert, Vlad}
• analitic (engl. intensional) prin enunțarea unei proprietăților comune tuturor unităților statistice, de exemplu, {x | x ∈ ℕ, x < 2} sau “persoanele domiciliate în Corabia la 1 ianuarie 2024”.

De regulă, nu avem acces la toate elementele unei populații, nici măcar ca nume, motiv pentru care o descriere analitică sugerează că vorbim mai probabil de o populație decât de un eșantion. 

Pe de altă parte, având acces limitat la populație, nu ar trebui să știm numărul de elemente (efectivul). Deci o descriere de forma “o mie de respondenți”, cu un efectiv clar precizat, sugerează abrevierea unei descrieri sintetice, și respectiv că descriem un eșantion. (Numărul precis demonstrează că am putea să îi identificăm pe fiecare din cei 1000, și, dacă spațiul ne-ar permite, să îi înșiruim.)

Și populația, și unitatea statistică ar trebui să fie clar definite, și fizic, și conceptual. Nu putem descrie o mulțime de nori dacă nu știm sigur unde se termină unul și începe celălalt. Uneori vom fi nevoiți să tragem o linie arbitrară, pentru a putea totuși descrie cumva realitatea înconjurătoare, însă acest proces trebuie să fie cât mai evident pentru restul utilizatorilor produsului statistic.

Variabile

Variabila (clasic caracteristică) este o însușire ce poate fi evaluată, la un moment dat, o dată și numai o dată pentru fiecare unitate statistică dintr-o populație. (De exemplu, averea unei persoane fluctuează în timp, dar are o valoare și numai o valoare numerică la momentul 1 ianuarie 2020.) Unii autori consideră că unele atribute, deși par caracteristice, nu sunt cu adevărat variabile pentru că nu pot lua decât o valoare. (De exemplu, numărul de capete al omului nu “variază”m deci probabil nu e variabilă.)

Mulțimile teoretice de numere (întregi, raționale, reale etc) sunt infinite, dar în statistică, aproape orice variabilă, fie ea și numerică. are multiple limitări. De exemplu, în sistemul românesc de învățământ, notele sunt de la 1 la 10. Numim întregii 1, 2, .. 10 valori posibile (clasic variante statistice) ale variabilei Notă.

Frecvent, unele valori posibile sunt foarte rare (de exemplu, 1 la desen). Numim variantele statistice care au fost cu adevărat prezente în populație valori caracteristice. Vom spune că 8 este valoarea caracteristică a variabilei Notă la desen pentru unitatea statistică “elevul Popescu”. În contextul variabilelor observate de mai multe ori în timp, mai numim valoarea caracteristică a unui variabile stare sau realizare (realization).

O relație 1➝1, în care fiecare unitate statistică are o valoare și doar o valoare pentru acel atribut, descrie, evident, o funcție, colectivitatea find domeniul, mulțimea variantelor statistice – codomeniul, iar mulțimea valorilor caracteristice – imaginea funcției.

Unii algoritmi statistici sunt dedicați analizei mai multor observații ale aceleași variabile, eventual pentru aceeași unitate statistică, la mai mult momente de timp. (De exemplu, populația României la 1 ianuarie 2020, 2021 etc.) În astfel de situații, unitățile statistice nu vor mai fi descrise doar cu numele, ci și cu data. Populația ar putea cuprinde “Orange SA la 1 ian 2020”, “Orange SA la 1 ian 2021”, “Orange SA la 1 ian 2022” etc. Analiza acestor serii de date cronologice pune accent pe diferențele de la o dată la alta.

Alte analize statistice analizează valorile caracteristice ale aceleiași variabile în distribuție geografică. De exemplu, am putea analiza populația județelor României în formă tabelară, dar modele mai sofisticate ar putea lua în calcul și distanțele / vecinătățile fiecărui județ.

În prima parte a semestrului 1, vom ignora relațiile temporale și spațiale. O variabilă apreciată în afara vecinătăților spațiale și a relațiilor temporale este numită atributivă. Înălțimea fiecărui student la data înmatriculării este o variabilă atributivă, un atribut al acelui student; însă înălțimea sa la vârstele de 10 ani, 11 ani, 12 ani, ar fi mai corect analizată ca serie de date cronologice. Aceeași variabilă, înălțimea, poate deci juca rol de variabilă atributivă sau cronologică, în funcție de modul cum au fost colectate datele (la un moment dat sau în serie cronologică).

Tipuri de scală

Datele atributive țin de regulă de unul din patru tipuri majore de variabilă. Cele mai simple variabile sunt cele nominale, adică acelea care sunt de facto nume, și nu admit direct niciun fel de operații aritmetice sau comparații. Fie că vorbim de numele propriu-zis al persoanelor, sau de sex, cu două valori posibile, “masculin” și “feminin”, vorbim în primă instanță de atribuirea, pentru fiecare unitate statistică, a unui cuvânt. În demografie, alte variabile ce nu admit operații aritmetice sau comparații sunt mediul urban / rural, starea civilă (celibatar / căsătorit / divorțat / văduv), și etnia / naționalitatea.

Un set de variabile sunt aparent nominale, însă permit ordonarea. De exemplu, clasificarea întreprinderilor în România ca mici, mijlocii sau mari are implicații și în analiza statistică. O diferență amplă între procentul de taxare va fi mai de înțeles la comparația celor două extreme (întreprinderi mici vs. întreprinderi mari), decât la comparații între “vecini” (de ex, mici vs mijlocii). Astfel, o analiză a perechilor de date de forma (tip de întreprindere după mărime, procent de taxare) va fi condusă altfel decât o analiză a datelor de forma (mediul întreprinderii, procent de taxare), în cel de-al doilea caz neexistând o ordine. Numim variabilele cu valori posibile ordonabile, dar care altminteri nu permit operații aritmetice, variabile ordinale.

O modalitate de a ne asigura că ordinea unor valori posibile nu este doar o convenție e să ne întrebăm dacă ordinea ar rămâne aceeași la trecerea în altă cultură (alfabet grec sau japonez, cuvinte în franceză, revenirea la RSR). Dacă ordinea persistă în aceeași formă la toate aceste transformări suntem siguri că avem o variabilă ordinală. În acest mod, devine evident că “numărul curent” este doar o convenție necesară unei tabel, adică o variabilă nominală.

Variabilele nominale și ordinale formează grupa variabilelor calitative, și nu permit adunări, scăderi, înmulțiri, nici între ele, nici cu constante. De partea cealaltă, variabilele cantitative sunt cele care permit operații aritmetice. 

Cele mai comune variabile cantitative sunt cele de tip raport (sau proporție), numite astfel deoarece putem descrie raportul a două valori. De exemplu, averea se poate dubla, ceea ce, cu alte cuvinte, înseamnă că averea din viitor este de 2 ori mai mare decât cea din trecut.

Excepția tipică de la tipul raport este temperatura în grade Celsius. Cu excepția temperaturii de precis zero grade, orice temperatură poate fi inclusă într-un calcul aritmetic, însă rezultatul împărțirilor nu va avea sens. De exemplu, dacă ieri au fost 2°C, iar azi sunt -4°C, nu putem spune că “temperatura a crescut de minus două ori”, afirmația fiind absurdă. Putem spune însă că temperatura a scăzut cu 6°C de la o zi la alta. Datele cantitative pentru care raporturile ar fi absurde se numesc date de tip interval (sau de tip cardinal). Fiind date cantitative, datele de tip interval permit anumite operații aritmetice – anume scăderile.

Pentru orice variabilă, dacă valorile posibile pot fi și pozitive, și negative, înseamnă că zero este doar un reper de conveniență, și nu absența completă. Temperatura de 0°C nu este ultima limită a temperaturii, dar greutatea de 0 kg este limită, neexistând obiecte de greutate negativă. Existența unui zero adevărat permite calcularea de raporturi și este caracteristică numai datelor de tip interval.

În epoca modernă, în care datele sunt stocate doar digital, orice informație devine număr, ceea ce permite ca orice să se adune sau să se împartă. Devine cu atât mai important ca statisticienii să decidă prin logică dacă o variabilă este cantitativă sau calitativă, și cărui tip îi aparține. O situație frecvent înșelătoare este cea a întrebărilor de chestionar “ce opinie aveți despre X?”, cu răspunsuri de forma “foarte de acord”, “moderat de acord”, “neutru”, “moderat în dezacord”, “deloc de acord” (așa numita scală Likert). Aceste date sunt stocate digital sub formă de întregi, 1 semnificând “foarte de acord”, 2 – “moderat de acord”, 3 – “neutru”, șamd. Este desigur tentant să operăm cu aceste numere ca și cum ar fi măsurători reale. De exemplu, am putea teoretic estima răspunsul tipic cu media aritmetică a acestor întregi de forma 1, 2, 3 etc. Dar, întrucât diferențele nu au sens, între 1 (“foarte de acord”) și 2 (“moderat de acord”) nefiind precis aceeași diferență ca între 2 (“moderat de acord”) și 3 (“neutru”), media aritmetică nu are sens. În realitate, fie că folosim răspunsurile în cuvinte, fie că folosim codurile numerice, răspunsul la o întrebare cu scală Likert este cel mult ordonabil. Scala Likert este deci una ordinală.

În sondajele reale, utilizarea variantei “Nu știu” transformă variabilele de pe scala Likert și alte scale aparent numerice în scale nominale. Deși majoritatea variantelor vor avea o ordine, per total, varianta “Nu știu” nu se încadrează în cea ordine. De regulă, pentru a putea analiza astfel de date ca și cum sunt ordinale, vor fi eliminate din setul de date răspunsurile din categoria / categoriile ce nu pot fi încadrate în secvența ordonată a răspunsurilor.

Similar, utilizarea de numere poate fi înșelătoare. Numerele sectoarelor nu oferă nici măcar posibilitatea ordonării, Sectorul 6 nefiind în fața sau în urma Sectorului 4, decât cel mult într-un tabel scris în modul cel mai lizibil.

Importanța tipului de variabilă în analiza economică

Pentru orice mărime cantitativă, scăderile au sens. Prin urmare, pentru astfel de variabile se vor defini sporuri (eng. difference sau absolute change), de la un moment la altul, ca diferențe de forma (valoare finală) minus (valoare finală). De exemplu, dacă pensia medie este azi 1100 de euro, dar în urmă cu un an era 1000 euro, spunem că s-a înregistrat un spor Δ de (X_final) – (X_inițial) = 1100-1000 = 100 euro de-a lungul acelui an. Pe de altă parte, dacă pensia medie trece de la 1000 euro la 900 euro, vom spune că s-a înregistrat un sport negativ, de -100 euro.

Numai mărimile de tip raport permit și împărțiri cu sens. Cea mai importantă împărțire din analiza economică este indicele (eng. relative change ratio, mai rar termenul ambiguu index), adică I = (X_final) / (X_inițial). Dacă pensia medie crește într-un an de la 1000 la 1100 euro, spunem că indicele de creștere a pensiei este 1100 / 1000 = 1,1. În comunicarea cu publicul vom spune că pensia actuală este 110% din valoarea precedentă.

Tot la variabilele de tip raport putem defini și ritmul (eng. rate of change), care descrie sporul în raport cu valoarea inițială, adică este Δ / (X_inițial) = (X_final / X_inițial) – 1. În aceeași trecere de la 1000 la 1100 euro, vom spune că pensia a crescut cu 10% față de valoarea precedentă. Indicele și ritmul sunt perfect sinonime, aceeași informație se transmite cu “valoarea finala este X% din valoarea inițială” sau cu “”valoarea finala este cu (X-100)% mai mare decât valoarea inițială”.

Majoritatea mărimilor economice au un zero adevărat, ceea ce permite interpretarea împărțirilor, și deci calculul indicelui și ritmului, însă există excepții.

Transformări de variabile

Variabilă surogat

Putem converti o serie de date calitativă în una cantitativă, la care, spre deosebire de Likert, numerele să aibă valoare de număr. Să considerăm merele lui Cezanne:

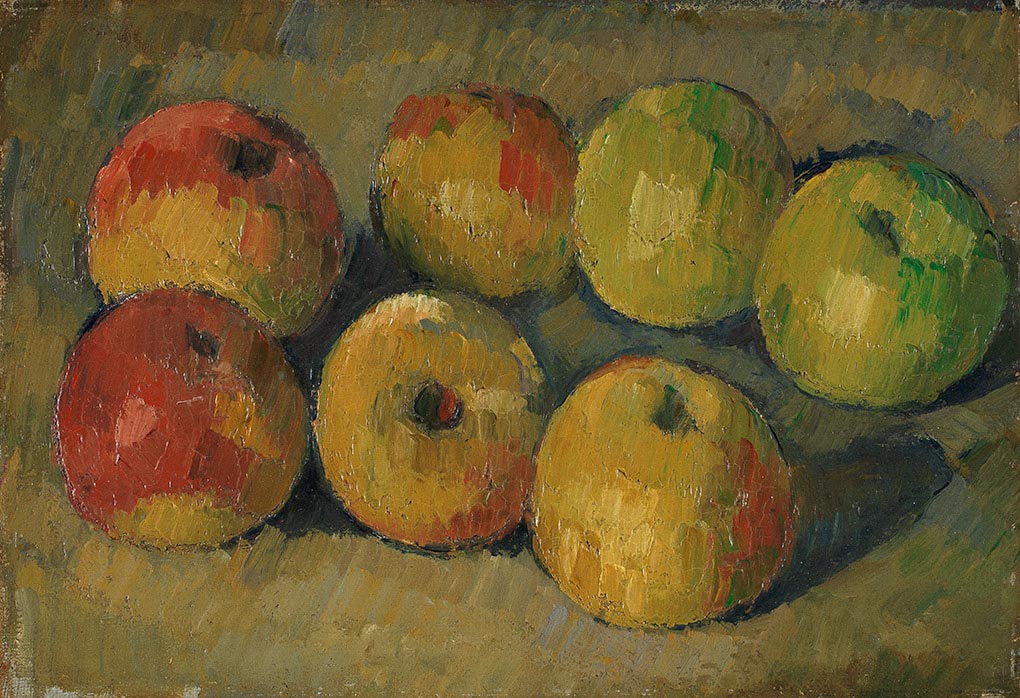
De la stânga la dreapta, cele din rândul de sus sunt roșu, (aproximativ) galben, verde, verde. În rândul de jos, de la stânga la dreapta, avem roșu, (aproximativ) galben, galben. Aceste date se tabelează tipic cu unitățile statistice pe linii, variabilele pe coloane și cheia primară în prima coloană.

Nr crt	Culoare
1	roșu
2	galben
3	verde
4	verde
5	roșu
6	galben
7	galben

Numărul curent este variabilă nominală. (Ordinea aparenta a numerelor 1…7 este aici una artificial impusă. Mărul notat în tabel cu numărul 4 nu este vecin în tablou cu mărul numărul 5. Puteam să le numerotez de jos în sus, sau imaginându-ne că merele sunt puse pe coloane. Prin contrast, vecinii de pe scala Likert, o scală realmente ordinală, sunt chiar vecini și nu pot fi permutați.)
Culoarea este și ea variabilă nominală. Așa cum se prezintă, ea nu este subiectul unor operații matematice. Putem însă să derivăm din ea variabile cu valoare numerică utilă, cu ajutorul unei propoziții. Astfel, în primă instanță, putem crea variabila derivată cuprinzând valoarea de adevăr a propoziției “acest măr este verde” pentru fiecare unitate statistică.

Nr crt	Culoare	Acest măr este verde?
1	roșu	NU
2	galben	NU
3	verde	DA
4	verde	DA
5	roșu	NU
6	galben	NU
7	galben	NU

Mai mult, am putea stoca aceste variante DA / NU în format binar, cu 0 însemnând de regulă fals, iar 1 – adevărat.

Nr crt	Culoare	Acest măr este verde?	Acest măr este verde? (0 = NU)
1	roșu	NU	0
2	galben	NU	0
3	verde	DA	1
4	verde	DA	1
5	roșu	NU	0
6	galben	NU	0
7	galben	NU	0

O variabilă cu doar două valori posibile se numește binară, alternativă sau dihotomică. O variabilă derivată, care codifică cu 0 și 1 informații derivate din altă variabilă, se numește variabilă surogat (eng. dummy). Variabilele surogat sunt un tip de variabilă binară.

Nu putem face împărțiri cu valori 0. Diferențele nu au sens real, pentru că 1-0 poate fi calculat, dar nu are sens (“mărul verde este mai mare cu 1 decât cel roșu”? în ce sens, pe ce măsură?). Nici măcar ordinea nu este logică, mărul verde nefiind înainte sau în urma celorlalte. De fapt, variabila surogat este nominală.
Cu toate acestea, dacă vom respecta regula de conversie “0 = nu și 1 = da”, vom obține valori numerice foarte utile, dar numai la nivel colectiv. Astfel, suma acestor numere este numărul (efectivul, eng. count) submulțimii de mere verzi (aici 2), iar media aritmetică a acestor numere este proporția din mulțime reprezentată de unitățile statistice ce îndeplinesc condiția. Aici, 2/7 ≈ 0,28 din întreaga mulțime de mere este ocupat de grupul merelor verzi. (În comunicațiile cu publicul, vom spune că 28% din mere sunt verzi.)

Discretizare

Există și operațiuni în sens opus, care transformă o variabilă numerică (și chiar cantitativă) într-una nominală. Astfel, să considerăm 5 întreprinderi cu numărul de angajați din tabelul de mai jos:

Nr crt	Efectiv de angajați
1	20
2	200
3	2000
4	100
5	60

Conform legislației din România, se definesc ca întreprinderi mici cele cu mai puțin de 50 de angajați, ca întreprinderi mari cele cu cel puțin 250 de angajați, și ca întreprinderi mijlocii restul (de la 50 la 249). Putem deci defini o nouă variabilă

Nr crt	Efectiv de angajați	Tip de întreprindere
1	20	Mică
2	200	Mijlocie
3	2000	Mare
4	100	Mijlocie
5	60	Mijlocie

Noua variabilă este una ordinală (nu permite operații aritmetice, dar permite comparații și ordonări). Trecerea de la numere precise la categorii numerice definite de intervale se numește discretizare (engl. binning).

Continuitate, extensivitate, aditivitate

Majoritatea variabilelor vor avea un domeniu limitat de valori posibile. Limitele pot fi uneori doar intuite (nu orice combinație de litere constituie un nume românesc valid), iar uneori sunt explicite (notele sunt de la 1 la 10). Variabila este practic o funcție, al cărei domeniu este populația, și al cărei codomeniu este mulțimea valorilor posibile.

Limitarea codomeniului este uneori dedusă din exprimarea sa ca interval, dar uneori vorbim și de limite în interiorul intervalului respectiv. Astfel, în catalog se trec numai note întregi, și deci valorile posibile sunt doar 1, 2, … 10, nu și numerele ne-întregi din intervalul [1; 10]. Numim variabilele care nu pot la decât unele valori din intervalul de valori posibile, dar nu pot lua valori intermediare, variabile discontinue (discrete).

Tehnic, sumele de bani nu pot fi divizate la infinit. Putem vorbi de o sumă de 1 leu, sau de una de 101 bani, dar, în mod normal, sumele bănești nu pot cuprinde fracțiuni de ban, precum 1,012 bani. Această limitare a sumelor bănești la numere întregi de bani are multiple implicații practice:

• La construcția unui formular digital, ar trebui să împiedicăm utilizatorii din a introduce fracțiuni de bani.
• La aritmetica financiară, ar trebui să utilizăm tipuri de date la care calculele sunt făcute cu precizia caracteristică numerelor întregi, pentru că altminteri vom obține erori.
• La raportarea publică a acestor date vom rotunji numerele absurde (“omul are în medie 1,99 picioare”).

Două comparații făcute în Python folosind numere care, transformate în binar, se scriu cu perioadă:

În afara comunicărilor către public, statisticienii vor fi tentați să considere orice o variabilă continuă, adică una care admite orice valoare intermediară.

O distincție utilă se mai face și între mărimile pentru care totalul pe mai multe unități statistice are sens, și cele pentru care totalul este cel mult un pas intermediar, fără înțeles în sine. Greutatea este aditivă în cel mai simplu sens. De exemplu, are sens să vorbim de totalul greutăților mai multor persoane care încearcă să ia liftul. Temperatura este nonaditivă, pentru că nu are sens să comunicăm suma temperaturilor din două locuri.

Majoritatea mărimilor aditive sunt extensive, în sensul că descriu o regiune din spațiul fizic (regiunea unde se extind). Regiunea de dezvoltare B-IF este reuniunea Bucureștiului cu Ilfovul. Astfel. efectivul populației regiunii B-IF este suma populației Bucureștiului și a populației Ilfovului; suprafața regiunii B-IF este suma celor două suprafețe etc. 

Prin contrast, temperatura se definește corect pentru fiecare punct de volum infinitezimal mic. Din geometrie știm că nu există două puncte adiacente, și deci nu putem construi regiuni (extinderi) în spațiul fizic ale punctelor pentru are se definește temperatura. Nu putem vorbi de temperatura regiunii B-IF, și nici măcar de temperatura Bucureștiului. Astfel de mărimi care diferă de la punct la punct sunt intensive, și nu sunt aditive niciodată. Nu vom comunica sume de mărimi intensive, deși uneori va fi posibil să calculăm media lor.

Estimație sau estimator?

Să considerăm cele 5 întreprinderi de mai sus. Un mod de a sintetiza, într-un singur număr, numărul de angajați este media aritmetică, (20+200+2000+100+60)/5 = 476. Spunem că, în medie, acele întreprinderi au 476, și înțeleg că numărul 476 este undeva între toate cele 5 numere.

Un alt mod de a calcula tendința centrală este mediana, adică valoarea de la mijlocul șirului ordonat de valori. Pentru a calcula mediana, este nevoie să sortăm șirul de date, de exemplu crescător: 20, 60, 100, 200, 2000. Valoare din mijlocul unui șir de 5 numere este a treia, adică 100.

Mediana poate fi adesea mai informativă decât media aritmetică. De exemplu, numărul median de picioare al omului este 2, un număr mai puțin ridicol decât media aritmetică de 1,999. Pe de altă parte, mediana 2 poate sugera că toți oamenii au 2 picioare. Media aritmetică și mediana sunt două modalități de a evalua tendința centrală a unei serii de numere, fiecare cu avantaje și dezavantaje.

Media aritmetică se obține prin câteva calcule aritmetice. Calcularea medianei necesită câțiva pași care nu sunt exprimabili în limbaj aritmetic (sortare, căutare la poziție dată). Ambele numere se obțin totuși urmând pași bine definiți. Mai mult, ambele au utilitate în statistica inferențială. Media aritmetică a unui eșantion este cel mai bună metodă de estimare a mediei aritmetice a populației mamă. Mediana eșantionului este o metodă de estimare a medianei populației.

Media și mediana populației, precum și orice alte proprietăți ale populației care nu sunt cunoscute direct, și sunt doar estimate din informația din eșantion se numesc parametri și se notează frecvent cu litere grecești.

Procedeul de estimare al unui parametru se numește estimator, indiferent dacă este o formulă matematică simplă sau rezultatul unui algoritm complex, și dacă are nume / notație sau nu. De exemplu, media aritmetică a eșantionului, calculată cu formula clasică a mediei aritmetice, este cel mai bun estimator al mediei populației.

Există estimatori mai buni sau mai slabi, de regulă asta însemnând mai potriviți situației sau mai nepotriviți. Calitatea estimatorului se apreciază în două moduri, cu referire la două tipuri de eroare. De exemplu, în cadrul pedagogic a cursurilor de statistică, vi se vor descrie două metode de estimare a dispersiei unui set de valori de tip interval. (Dispersia este un mod de a cuantifica variabilitatea.) Unul din ele obține estimații mai mult sau mai puțin apropiate de valoarea pe care o estimează, numită dispersia populației. Uneori estimațiile obținute prin această metodă sunt mai mici decât valoarea reală, alteori sunt mai mari, dar în medie, ele sunt aproximativ egale cu parametrul pe care încearcă să îl estimeze. Spunem că acest tip de eroare este unul nesistematic. Prin contrast, celălalt estimator va da valori în medie mai mici decât parametru pe care îl estimează. Cu alte cuvinte, cel de-al doilea estimator subestimează parametrul. Spunem despre subestimările persistente, ca și despre supraestimările persistente, că sunt erori sistematice. Eroarea sistematică se mai numește deplasare (eng. bias). Ar fi deci ideal ca estimatorii să fie nedeplasați.

Seria de date

Valorile caracteristice dintr-o populație se pot scrie ca serie. O serie este un grup de valori, la care fiecărui element i se atribuie și un identificator unic. De exemplu, populațiile fiecărui județ formează o serie, dacă sunt descrise sintetic (extensional), și se cunoaște pentru fiecare din ele, județul căreia în corespunde. Chiar și înșiruirea “Alba”, “Arad”, “Bacău”,… constituie o serie de date, în acest caz pe scală nominală. Descrierea completă a unei variabile, sub formă de serie, este numită și serie de date univariată.

Mai frecvent veți opera cu tabele cu valori pentru mai multe variabile. De exemplu, pentru fiecare județ, puteți preciza un triplet de valori caracteristice, cuprinzând numele, populația, și suprafața. Descrierea simultană a mai multor variabile formează o serie de date multivariată (sau multidimensională). Chiar și la nivelul cursului de statistică introductivă, numărul de valori caracteristice dintr-o serie de date va fi suficient de mare încât să preferați enumerarea fiecărei variabile pe câte o coloană, cu valorile înșirate pe rânduri consecutive. În acesta aranjament, fiecărei unități statistice i se va aloca o linie. În software statistic ca R, această “linie” se numește observație, iar în teoria bazelor de date, se numește n-tuplu (de la dublu, triplu, cvadruplu, cvintuplu etc).

O mulțime de valori caracteristice, cum sunt numerele \(\{Populație_{Alba}, Populație_{Arad}, \dots ,Populație_{Zalău}\}\), nu are neapărat o ordine. În acest exemplu, le putem prezenta în ordine descrescătoare / crescătoare a valorilor, dar și în ordinea alfabetică a județelor. Ordinea lor este deci arbitrară, spre deosebire de noțiuni ca “întreprindere mică”, “întreprindere mijlocie” și ” întreprindere mare”, care pot fi ordonat doar într-un singur mod crescător. Deci, de regulă, valorile caracteristice dintr-o serie de valori caracteristice vor putea fi ordonate în câteva moduri, la fel de pertinente. Seriile de date unidimensionale sunt deci un tip de ansamblu intermediar, între șirul algebric, ansamblul strict ordonat, și mulțime, adică ansamblul fără nicio ordine.

Pentru stocare sau prezentare, analistul va trebui să aleagă una din multiplele opțiuni de ordonare a valorilor caracteristice. Alegerea poate fi arbitrară; de exemplu, în funcție de context, pot prefera să ordonez efectivele populațiilor județene crescător, sau descrescător. Însă o dată stabilită o ordine, mulțimea de valori caracteristice nu mai este doar o mulțime, ci devine un șir. Adesea, chiar și fără a fi decis o ordine, vom presupune că această ordine există, astfel încât seria de date devine un vector, adică o înșiruire ordonată. În această situație, a ordinii decise sau prezumate, fie ea oricât de arbitrară, vom descrie ansamblul de valori unei variabile așa cum descriem orice șir ordonat din algebră, cu paranteze rotunde:

• fie sintetic cu \( (x_1, x_2 \dots x_n) \), unde n este numărul de unități statistice
• fie analitic ca \( (x_i)_{i=1^n} \).

Șirul ordonat, chiar și ad hoc, se abreviază cu bold-italic, ca în \(\boldsymbol{x}\).

Dacă variabila este cantitativă, șirul de valori caracteristice va fi uneori folosit și ca matrice cu o singură coloană. În aceeași situație, pur numerică, o serie de date multidimensională va fi o matrice (eng. design matrix sau data matrix), cu fiecare variantă pe câte o linie și fiecare unitate statistică pe câte o coloană. În afară de descrierea sintetică a matricii cu paranteze pătrate, despre care ați aflat la algebră, se mai practică notațiile

• \( [ \boldsymbol{x}_1, \boldsymbol{x}_2 \dots \boldsymbol{x}_m ] \) unde \(\boldsymbol{x}_j\) sunt vectori descriind câte o variabilă, iar m este numărul de variabile
• \( (x_{i,j})_{i=1,\dots,n;\, j=1,\dots,m}\)

Matricea, cu unitățile statistice ordonate pe linii și cu variabilele ordonate pe coloane, chiar și cu ordonări ad hoc, se abreviază cu bold, ca în \(\mathbf{x}\). Fiecare linie din matrice corespunde deci unei unități statistice și respectiv unei observări (eng. observation sau case). Fiecare coloană corespunde unei variabile (eng. variable sau feature).

Dacă valorile nu sunt doar cantitative, nu putem folosi calculul matricial, dar principiile de organizare de mai sus rămân valabile. Tabelul cu variabile pe o dimensiune și unități statistice pe cealaltă se va numi masiv de date (arhaic, bază de date). Un masiv de date este o structură conceptuală; pentru ca masivul să existe, nu este necesar să îl tipărim sau să îl afișăm “pe coloane și linii”, ci doar să îl imaginăm ca atare. (Faptul că memoria digitală este unidimensională nu vă împiedică să concepeți, să stocați și să utilizați matrici bidimensionale din RAM.)

Este recomandabil ca orice tabel, digital sau letric, să conțină o coloană de identificare unică a fiecărei unități statistice, asemănător cheilor primare din bazele de date. Uneori aceste coloane sunt deja create de circumstanțe; de exemplu, un tabel cu cetățeni români ar putea conține CNP-ul, care ar identifica fără echivoc o persoană. În lipsa acestei variabile de identificare, putem crea noi o coloană de identificare unică, cea mai simplă fiind “numărul curent”.

Serii de date strict ordonate

În seriile de timp, indicele (indexul, în jargon informatic) folosit la enumerarea valorilor caracteristice are o ordine clară.

În cazul seriilor de timp numite de moment, fiecare valoare caracteristică este înregistrată la un anumit moment. De exemplu ordinea datelor din seria \(\{Pensie\ medie_{1\ ian 2020}, Pensie\ medie_{1\ ian 2021}, \dots, Pensie\ medie_{1\ ian 2025}\}\) este non-ambiguă.

De regulă, variabilele de moment descriu mărimea unei variabile fluctuante la acel moment, situație în care se numesc variabile de stoc (eng. stock variables). Stocul nu este neapărat unul fizic. Temperatura din fiecare moment este o variabilă de stoc, fiind o variabilă fluctuantă de la moment la moment.

În cazul seriilor de timp de interval, fiecare valoare se referă la o perioadă de timp. De exemplu, putem vorbi de \( \{Creșterea\ pensiei_{1\ ian 2020 \rightarrow 1\ ian 2021}, Creșterea\ pensiei_{1\ ian 2021 \rightarrow 1\ ian 2022}, \dots , Creșterea\ pensiei_{1\ ian 2024 \rightarrow 1\ ian 2025} \} \). Și în acest caz, vom putea ordona valorile cronologic, dacă vom defini intervale similare (doar lunare, sau doar anuale etc).

Unele variabilele de interval, numite variabile de flux (eng. flow variables), descriu variația unei variabile de stoc. De exemplu, numărul de emigranți dintr-un an este calculat ca diferența dintre efectivul populației la 1 ianuarie și efectivul populației la 31 decembrie, după ce am luat în calcul nașterile și decesele. Alte variabile de interval sunt de fapt variabile de stoc, sintetizând într-un singur număr mai multe valori caracteristice de stoc. De exemplu, efectivul mediu al populației într-un an este media aritmetică a celor 365 de efective din fiecare zi. Atât mediile stocurilor, cât și fluxurile nu pot fi definite pentru un anume moment, ci numai pentru un interval de timp.

Seriile de timp sunt singurele date adecvate pentru a calcula variabile derivate de dinamică, precum sporul, indicele și ritmul, descrise mai sus. Variabilele de stoc au întotdeauna spor, iar dacă sunt de tip raport, pot fi folosite și la derivarea de indici sau ritmuri. Variabilele de flux au de regulă un zero real, indicând un stoc neschimbat, și ar trebui să fie adecvate calculării de sporuri, indici și ritmuri, condiția fiind din nou utilizarea de intervale similare. Este neclar ce exprimă propoziția “numărul de emigranți din 2021 este de 10 ori mai mare decât cel din ianuarie 2022”. Dacă luna ianuarie ar fi de regulă o lună mai comună pentru migrație, comparat cu celelalte luni, ar fi de așteptat să aibă mai mult de o doisprezecime din totalul anual, dar tot nu e clar daca 1/10 e mult sau puțin comparat cu așteptările. Prin contrast, putem intui clar sensul propoziției “numărul de emigranți din ianuarie 2021 este dublu celui din ianuarie 2020”.

În seriile de date spațiale, relațiile sunt chiar mai complexe, o unitate statistică învecinându-se cu mai multe de două alte unități statistice. În multe situații, va fi mai bine să includem poziția și vecinătatea în analiza noastră, în loc să tratăm variabilele ca pur atributive.

Prin contrast cu datele ordonate cronologic, celelalte tipuri de observații se vor face, pe cât posibil, la același moment. Este relativ absurd să comparăm populațiile țărilor din Europa folosind, pentru unele din ele date din 2020 și pentru altele, date din 2000. Numim colectarea de date de-a lungul timpului, ca în seriile de timp, observare longitudinală, iar observarea simultană – observare transversală (eng. cross-sectional). Combinația acestora, adică colectarea la mai multe momente succesive, a câte unui set de date transversale, despre aceleași unități statistice, generează seturi de date de tip panel (de ex., populațiile țărilor lumii în 2010, apoi în 2011, apoi în 2012 etc).

Relativ vs absolut

În contextul statisticii, “relativ” se referă la o măsură ce se definește doar în raport (“relație”) cu alte măsuri. De exemplu, calculul sporului anual al pensiei până la 1 ianuarie 2020 va necesita și cunoașterea valorii pensiei la 1 ianuarie 2019. Spunem că acest spor este definit la 1 ian 2020 în raport cu valoarea de la 1 ian. 2019. “Raport” nu se referă aici la împărțire, ci este sinonim cu “relație”.

Pensia de la 1 ianuarie 2020 poate să fie descrisă fără a ne referi la alte valori ale pensiei sau ale altor variabile, dar sporul, ritmul sau indicele pensiei necesită cel puțin încă o valoare a pensiei. Sporul, ritmul și indicele sunt deci mărimi relative, dar valoarea de la un anumit moment nu este relativă. Mărimile care nu sunt relative se numesc absolute. Nici absolut nu se referă la valoarea absolută (modul), ci doar la independența acelei mărimi de altele.

În contextul variabilelor, deosebim câteva tipuri de variabile relative.

• Variabilele relative de structură descriu distribuția internă a unui întreg, respectiv componentele sale. Cu alte cuvinte, vorbim de proporții, fie ele numere între 0 și 1, sau echivalentul lor în scriere procentuală, care va fi cuprins între 0% și 100%..
• Variabilele relative de dinamică sunt cele care cuantifică schimbarea în timp (spor, indice, ritm). Pentru a le calcula, vom observa același fenomen de două ori, la momente diferite.
• Variabilele relative de coordonare cuantifică discrepanța dintre două mărimi măsurate simultan, pentru unități statistice distincte. De exemplu, pornind de la valorile absolute ale PIB-ului României din 2022 (240 mld EUR) și PIB-ului Ungariei (160 mld EUR), vom putea calcula, ca mărimi relative ale PIB-ului României în relație cu cel al Ungariei:
  • diferența (80 mld EUR)
  • raportul (de 1,5 ori mai mare).
• Variabile relative de intensitate sunt variabile intensive, obținute din două mărimi măsurate simultan pentru aceeași unitate statistică. Ele se calculează de regulă când îmbunătățesc comparațiile întru unități statistice. De exemplu
  • România avea la finalul lui 2020 cca 19 milioane locuitori, ceea ce corespunde unui PIB pe cap de locuitor de 240 mld EUR / 19 mil ≈12,630 EUR/locuitor.
  • Ungaria avea cca 9 milioane locuitori, ceea ce corespunde unui PIB pe cap de locuitor de 160 mld EUR / 9 mil ≈ 17,780 EUR/locuitor, ceea ce indică productivitate mai mare pentru maghiarul mediu, comparat cu un român mediu.

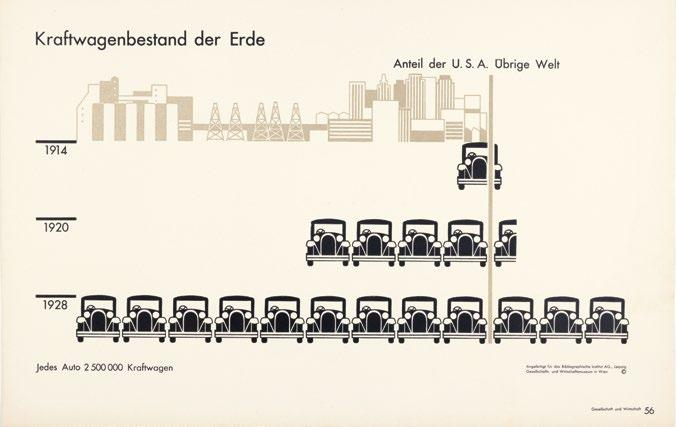
Variabilele de coordonare sunt utile și în comunicarea cu publicul. Graficele numite isotype, popularizate de Neurath, ilustrau încă de acum 100 de ani

• cum numărul de autovehicule din lume a crescut de 4,5 ori între 1914 și 1920 (un indice, deci variabilă de dinamică),
• și cum, în 1920, în SUA erau de 8 ori mai multe autovehicule decât în restul lumii (jumătate de vehicul vs 4 vehicule; variabilă de coordonare):

Indicatorul statistic

Indicatorul statistic este sintagma ce combină un număr (de exemplu, 205 miliarde), o unitate de măsură (EUR) și descrierea completă (așa zisa determinare noțională). În aceste exemplu, indicatorul ar fi “datoria externă a României la 1 ianuarie 2025 a fost 205 miliarde EUR”. Determinarea noțională are trebui includă, în cazul în care sunt aplicabile, locul, momentul sau intervalul, metoda de măsură, metoda de eșantionare, metoda de sintetizare. Fiecare dintre aceste informații ar trebui oferite interlocutorilor fără a aștepta cereri din partea lor, mai ales dacă pot exista dubii. De exemplu, propoziția “datoria externă a României a fost 205 miliarde EUR” este neinformativă în lipsa enunțării momentului.

Indicatorii sunt de două tipuri:

• statistici (substantiv articulabil), adică rezultate precise, fixe ale statisticii descriptive
• estimații, adică rezultate ale statisticii inferențiale, în scop de previziune și cu caracter probabilistic.

O statistică este deci

• fie rezultatul observării totale a populației (“populația României la recensământul din 2022 a fost 19.053.815 locuitori”)
• fie rezultatul tratării unui eșantion ca și cum ar fi o populație (“sondajul a cuprins 1100 respondenți”).

Ambele propoziții au caracter precis, și se pot contrasta cu indicatorii-estimare de forma “populația României după domiciliu, estimată de INS la 1 ianuarie 2025 a fost 21739,4 mii persoane”.

Deci indicatorii sunt utili

• la rezumarea (“măsurare”) a datelor din eșantioane și din populații observate total
• la estimare și la verificarea ipotezelor statistice, pentru populații observate parțial
• la comparare, în ambele cazuri.

Ipotezele statistice sunt propoziții propuse spre validare sau invalidare, care se referă la parametri. Așa cum nu cunoaștem cu precizie, și doar estimăm, parametrii, ipotezele statistice nu vor fi confirmate sau infirmate cu certitudine. De exemplu, statistica inferențială ne va permite să ne pronunțăm asupra ipotezei “vârsta medie a românilor diferă semnificativ de 20 de ani”, într-un cadru probabilistic (“acceptând o probabilitate de 1% să greșim, vom considera că afirmația propusă este adevărată”).

Datele statistice primare sunt acele date care provin direct din dispozitivul de măsură (aparat, chestionar etc). Dacă datele au suferit modificări, fie de prelucrare primară, fie de analiză, vorbim de date secundare, indiferent dacă modificările sunt făcute de noi sau de persoana care ne-a oferit datele. Astfel, dispozitivele de măsură sunt întotdeauna surse primare, iar publicațiile statistice sunt întotdeauna surse secundare. Utilizarea datelor secundare ne expune riscului de a prelua erori în analiză.

Forme de prezentare a rezultatelor statisticii descriptive

În cursul observării, deosebim

• lista, un document care precizează același tip de informații / aceleași variabile pentru toate unitățile statistice din studiu
• fișa, un document care stochează informații despre o singură unitate statistică, în format standardizat, astfel încât setul complet de fișe să permită construirea unei liste.

Tabelul este un aranjament 2D al rezultatelor unei analize statistice, cuprinzând

• valorile caracteristice
• descrierile, sub formă de text, a ce reprezintă acestea (etichete de coloană și linie; eng. headers)
• macheta, adică liniile care separă textul
• titlul și / sau notele de la baza tabelului (eng. caption) care vor include, printre altele
  • numărul tabelului, pentru identificarea în document
  • subiectul tabelului, adică populația descrisă
  • predicatul tabelului, zis și sistemul de indicatori, adică descrierea variabilelor
  • sursa datelor.

Graficul (chart, pentru imagini simple; plot, pentru scenariile mai complexe) este construcția geometrică ce permite transmiterea unui număr mare de date într-un mod intuitiv, pe un spațiu tipografic limitat sau pe dispozitive de vizualizare electronice de dimensiuni comune. Graficul cuprinde

• reprezentarea propriu-zisă a datelor (puncte, segmente, bare etc)
• axe și rețea (eng gridlines)
• gradații pe axe (eng. ticks), scară de reprezentare, sau ambele
• elemente de text (titlu general, titlu de axe, etichete de puncte, legendă, note).

Titlul sau notele ar trebui să specifice numărul figurii și sursa datelor.

Cel mai frecvent folosite grafice sunt cele bidimensionale, cu două axe perpendiculare între ele, adică cu un sistem de coordonate ortogonale (zise și rectangulare).

Tipuri de observare sau raportare statistică

Sondajul este cea mai comună formă de observare parțială, constând în selectarea, cât mai aleatorie, a unui eșantion de unități statistice, ulterior supuse unei forme standardizate de observare detaliată. De exemplu, în sondajele sociologice, participanții sunt selectați în parte aleatoriu (de exemplu, localitatea în care va fi aplicat chestionarul nu este aleasă complet la întâmplare!), iar întrebările vor fi aceleași pentru toți participanții. Standardizarea are rolul de a ușura analiza, dar și de reducere a costurilor.

Fundamentul matematic al analizei sondajelor este perfectat pentru sondaje complet aleatorii și cu revenire (eng. replacement), adică unul în care fiecare unitate statistică selectată pentru a fi parte din eșantion păstrează o șansă egală de a mai fi selectată. De exemplu, un sondaj al bilelor dintr-o urnă este cu revenire, dacă se extrag pe rând, câte o bilă, iar după citirea conținutului bilei selectate, ea este repusă în urnă. Sondajele cu revenire se mai numesc bernoulliene.

În cazul populațiilor mari, șansa de a extrage din nou aceeași unitate statistică este infimă, motiv pentru care sondajele sunt sociologic sunt efectuate fără revenire, adică nu vom re-chestiona o persoană care a fost deja selecționată și chestionată în cursul aceluiași sondaj. Chiar și sondajele fără revenire se pot conduce în manieră aleatorie. Cu toate acestea, în sondajele sociologice se practică câteva metode de simplificare a selecției, care diminuează semnificativ caracterul aleator al sondajului.

Un sondaj stratificat este unul care preîntâmpină o problemă de reprezentativitate, prin construirea unei stratificări a populației, și sondajul independent al fiecărui strat. De exemplu, un sondaj despre calitatea vieții studenților, condus numai la universități tehnice, va atrage în principiu, un număr mare de respondenți masculini și unul mai mic de respondente. Rezultatele unui astfel de sondaj dezechilibrat vor reflecta calitatea vieții studenților (masculin), nu a studenților în general. Pentru a contracara acest neajuns, se practică planificarea sondajului în mod separat pe studenți și pe studente. De exemplu, operatorii de teren pot fi însărcinați să chestioneze un număr egal de studenți și studente. Spunem că am stratificat populația pe sexe, și că am efectuat un sondaj separat pe stratul masculin și altul pe stratul feminin, urmând a combina răspunsurile în cursul analizei.

Un sondaj pe cuiburi (cluster) este o altă metodă de împărțire a populației în cursul perioadei de planificare a sondajului, motivația fiind de regulă una financiară. De exemplu, putem efectua un sondaj care să descrie atitudinile întregii țări, dacă ne limităm la câteva județe bine alese. Motivația este că vom avea nevoie de mai puține centre de colectare a chestionarelor. Riscurile sunt semnificative – este foarte probabil ca cele câteva județe să nu reprezinte toate tipurile de percepție.

O selecție mecanică este un alt procedeu de selecție nealeatorie folosit în cazul în care constituie o alternativă mai ieftină sau mai facilă la selecția aleatorie, atunci când suspectăm că rezultatele sale nu vor fi semnificativ diferite de cele ale unui sondaj aleatoriu. Cel mai simplu procedeu de selectare mecanică este cel în care agentul de teren va contacta persoanele de la fiecare a n-a clădire (de exemplu, de la fiecare a cincea clădire). Se poate introduce un element aleatoriu în acest proces prin tragerea la sorți a primei unități selectate. (De exemplu, putem trimite agentul la numerele 1, 6, 11, 16 etc, sau la numerele 2, 7, 12, 17 etc)

Ancheta statistică este o colectare de date detaliate, pe multe dimensiuni (variabile), despre un număr mic de unități statistice. Monografia statistică este un raport amplu, cu informații din diverse perspective, despre același domeniu economic sau regiune geografică. Ancheta de opinie este aplicarea unui chestionar amplu pe un grup de subiecți relativ mic și selectat nealeator.