Cuvântul “statistică” are mai multe înțelesuri. Cel de bază este cel de inventar, sau tabel de recensământ.

O serie de reguli generale se aplică la astfel de tabele. Este ideal ca fiecare linie să descrie un element al unei mulțimi, ca de exemplu, o persoană, în cazul recensământului. Fiecare coloană are trebui să descrie un tip de informație. De exemplu, o coloană are trebui rezervată numelor, alta – date de naștere etc.

Aceste reguli rămân valabile când tabelul este foarte înalt sau foarte lat, nemaiexistând în forma pe hârtie. În realitate, pe suport digital, este chiar mai important ca datele să fie bine organizate. Computerele sunt adesea un pas înainte în organizarea de tabele, limitând tipul de date introduse. (De exemplu, chiar și în Excel, coloana “dată de naștere” poate fi programată să nu accepte decât date, sau, mai strict, doar date din ultima sută de ani.)

Pe scurt, ca tehnică de bază, statistica este un grup de tactici de tabelare a informațiilor despre obiecte identificabile, tangibile sau intangibile, aparținând aceleiași clase logice.

Listele complete și informațiile ce sintetizează astfel de liste sunt produsele statisticii descriptive. De exemplu, în forma cea mai simplă, rezultatele unui recensământ sunt descrise ca număr total de indivizi. Astfel, Republica Romană avea un efectiv de cca. 300 de mii de locuitori la recensământul din 252 î.C. Dar la același nivel de precizie și simplitate se pot construi descrieri mai complicate. Graficul de mai jos, având timpul ca index, este numit cronogramă. În ciuda complexității aparente, cronograma de mai jos este doar o descriere, și este deci tot din sfera statisticii descriptive.

Prin urmare, al doilea înțeles al cuvântului “statistică” este statistica descriptivă, adică un grup de proceduri prin care datele din enumerări sunt sintetizate, obținându-se efective, medii, dispersii, histograme, coeficienți de corelație, curbe de regresie, cronograme etc.

Un al treilea tip de statistică este cea care deduce, pe baza informațiilor tabelate, informații despre alte entități, absente din acel tabel. Astfel, pe baza datelor despre numărul de nașteri și decese din ultimele decenii, putem estima care va fi populația unei regiuni în următoarele decenii. Folosind datele dintr-un eșantion de cca 1000 de alegători, estimăm preferințele de vot ale întregului corp electoral al unei națiuni. O aplicație cu flux informațional similar este cea în care statisticianul evaluează, în termeni probabilistici, scenarii din perioade sau regiuni despre care nu avem informații, pe baza unui set de date similare. De exemplu, pe baza numărului de nașteri și decese din ultimele decenii, putem evalua cu încredere 95% ipoteza că populația României va fi sub 20 de milioane la finalul acestui secol.

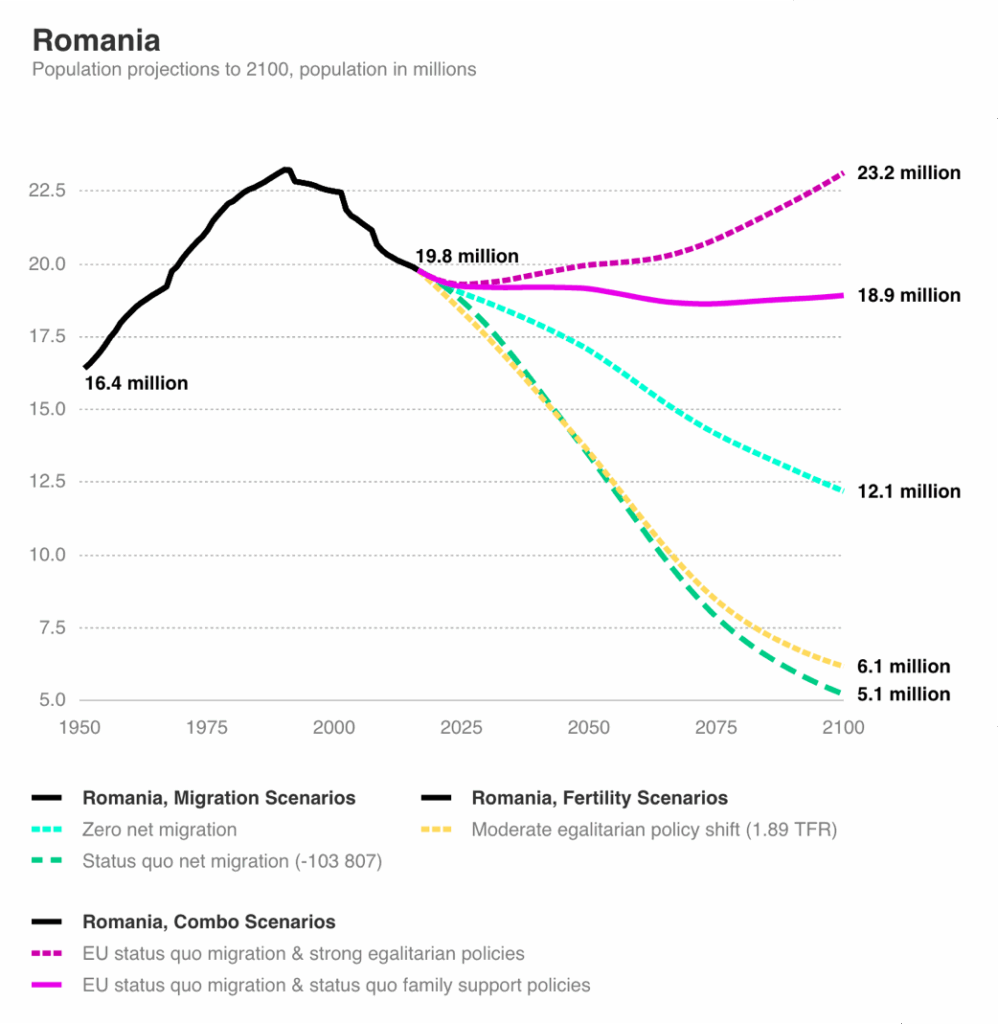
Deci, al treilea înțeles al statisticii, și pasul la problema de liceu la cea de facultate, este ramura statisticii numită statistică inferențială, adică grupul de proceduri prin care datele empirice sunt folosite ca estimatori ai unor indicatori populaționali și / sau ca putere de sprijin a unor ipoteze, de regulă folosind limbaj probabilistic.

O dată stăpânite procedeele statisticii inferențiale, veți putea contribui la ceea ce statistica are mai valoros de oferit societății. Alegerea celui mai potrivit coechipier care să primească pasa de gol într-un anumit scenariu, stabilirea numărului de brazi de Crăciun pe care îl poate vinde proprietarul unui magazin și a prețului corect pentru a evita rămânerea cu stocuri pe 1 ianuarie, alegerea numărului maxim de vize pentru imigranți în așa fel încât salariile localnicilor să rămână neafectate – toate sunt decizii ce se pot lua mai bine cu ajutorul statisticienilor. Statistica macroeconomică și statistica demografică sunt domenii de studiu importante ale educatorilor din Academia de Studii Economice, în care tehnicile inferențiale devin utile stabilirii de politici de stat. Discutăm la seminare rolul fundamental al articolului lui David Card în atingerea unui cvasi-consens în SUA privind lipsa de efect a imigrației asupra veniturilor localnicilor.

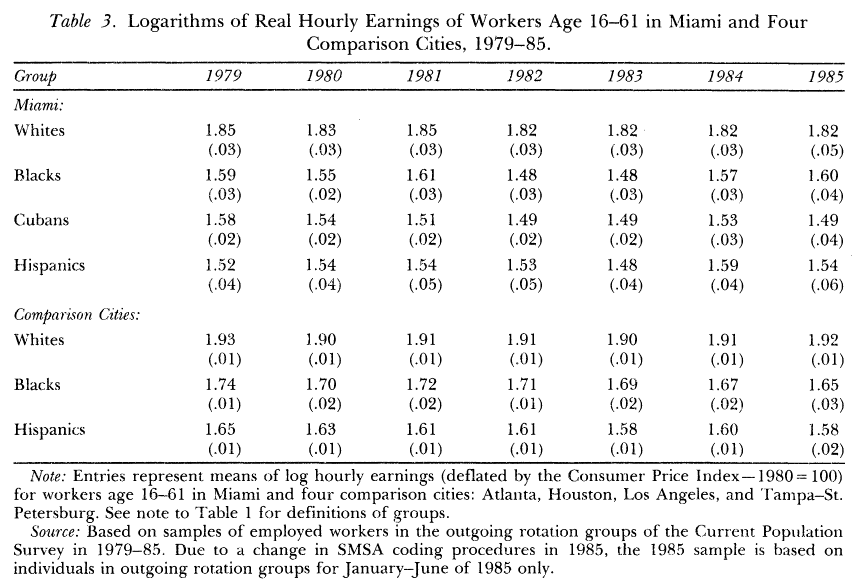
Acest articol este și subiectul este unuia din multele situații în care statisticienii intră în conflict cu factori de decizie, fie ei politicieni sau manageri din domeniul privat. Rezultatele studiului lui Card au fost contestate, fără motiv, de președinte al Sistemului Rezervei Federale a Statelor Unite.

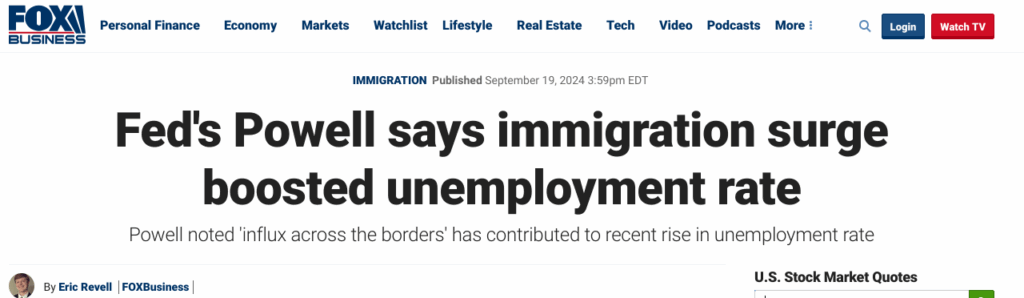
Astfel de conflicte nu pot să se încheie cu compromiterea acurateții datelor statistice, situație în care credibilitatea acelui statistician ar fi permanent pierdută, și expertiza sa nu ar mai fi solicitată. Din acest motiv, este ideal ca statisticianul și clientul său să nu se afle într-un raport de subordonare. În situațiile în care această subordonare este inevitabilă, cu precădere în instituțiile statistice de stat, regulile sunt ca statisticienii să lucreze cu precădere sub conducerea altui statistician și într-un cadru stabilit de statisticieni.

Shoot:	Chaser:

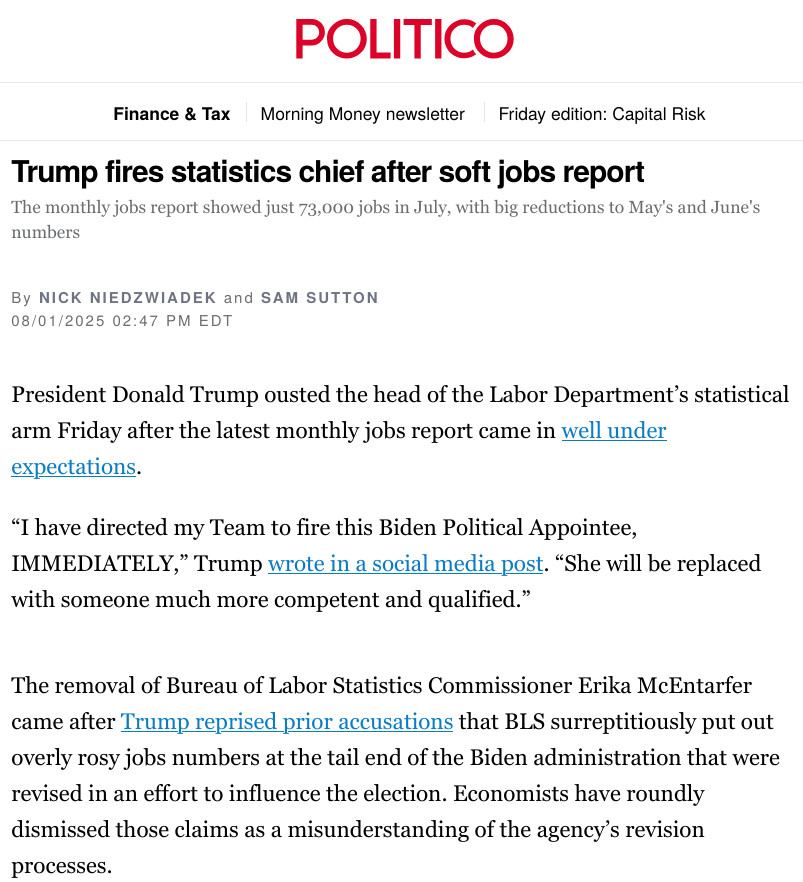O situație asemănătoare se descrie și în cazul statisticilor oficiale din România:

Faptă:	Răsplată:

Multe alte domenii științifice (biostatistica, genomica, termodinamica, fizica cuantică) adaptează metodele generice ale statisticii inferențiale la nevoile domeniului respectiv.

Istoria statisticii cuprinde personaje ale căror nume se vor tot repeta de-a lungul semestrelor. Majoritatea acestora au pornit de la date din domeniile lor de expertiză: Halley tabela durata vieții oamenilor, Quetelet calcula mediile Indicelui de Masă Corporală, Gauss descria abaterile măsurătorilor astronomice de la valorile așteptate, Galton cuantifica asemănarea dintre înălțimea taților și cea a fiilor, Fisher investiga ce tehnici agricole produc recolte superioare. Statistica matematică este acea ramură a statisticii care dezvoltă și validează metodele de descriere și de inferență. Deși Academia de Studii Economice este dedicată statisticii aplicate, unii dintre predecesorii noștri au propus indicatori statistici inovatori la momentul propunerilor lor, cel mai important fiind entropia informațională Onicescu.

Obiectul și metodele statisticii

Este deci evident că statistica studiază, în modul său particular, cu metodele sale generale, orice aspectele cantitative al unui fenomene măsurabil, aparent descris de alți specialiști (economiști, demografi, sociologi, fizicieni, chimiști etc), câtă vreme aceste aspecte se supun unor legi stocastice.

Un proces stocastic este unul care se desfășoară aparent la întâmplare, însă supus unor reguli matematice. De exemplu, nu putem prevedea dacă o singură aruncare a unei monede va duce la “cap” sau “pajură”; dar o monedă echilibrată, aruncată de foarte multe ori, va arăta “cap” în circa jumătate din încercări. Pe baza teoriei probabilităților putem demonstra, matematic, că cel mai frecvent, la 1000 de încercări, vom avea 500 de “capete”. Mai mult, putem calcula, de câte ori, la repetiția celor 1000 de încercări, vom obține doar 499 de “capete”, doar 498 de “capete” șamd

Pentru scenarii de la cele mai simple, precum moneda sau zarul, până la variațiile datelor astronomice analizate de Gauss, statisticienii au dezvoltat ecuații matematice ce permit un anumit nivel de previzionare. Este adevărat că statisticienii nu pot spune dacă moneda aruncată o dată va arăta “cap” sau “pajură”, și nici măcar câte “capete” vor fi arătate la următoarea aruncare de o mie de ori, dar pot descrie, pe baza modelelor din teoria probabilității, atât cel mai probabil rezultat, cât și o dimensiune a incertitudinii pentru previziunile lor.

Legile stocastice sunt deci reguli matematice fixe despre aspectele previzibile ale unor evenimentelor aleatoare, dezvoltate ca extensii ale teoriei generale a probabilității. Pentru statistica introductivă sunt importante două astfel de legi:

• Legea numerelor mari prevede că frecvența practică de apariție a unui eveniment “tinde” către probabilitatea lui teoretică de a se produce.
• Teorema limitei centrale prevede că, dacă repetăm serii de măsurători, mediile fiecărei serii vor urma anumite reguli matematice, indiferent de modul în care variază măsurătorile individuale.

Cuvântul aleator provine de la termenul latin “alea” (zar). Echivalentul său englez, random, provine de la termenul francez “randonnée” (plimbare lungă fără o anume destinație). Prin contrast, stocastic provine de la grecescul “stochastikos”, însemnând “priceput la a ținti” (ulterior “priceput la a ghici”). Așa cum unele lucruri nu pot fi deocamdată măsurate, unele fenomene la întâmplare (aleatorii) nu se supun, aparent, niciunei reguli matematice. Fenomenele care nu sunt obiectul legilor stocastice nu pot fi studiate nici de statistică.

Metodele statisticii sunt deci observarea, prelucrarea și analiza fenomenelor stocastice, în orice formă adecvată tipului de date în discuție. De exemplu, pentru statistica demografică, putem folosi, printre altele, recensământul populației ca observare, eliminarea chestionarelor unde vârsta este peste 120 de ani ca prelucrare, și calcularea efectivelor pe județ, sex și vârstă ca metodă de analiză. Pentru datele astronomice, metodele statistice vor diferi.

Modelul statistic

Așa cum, de facto, nu există nici planul înclinat ideal din manualele de fizică, nici sfera perfectă din geometrie, nici fenomenele din natură nu vor reflecta întotdeauna legile stocastice care ar trebui să le prezică comportamentul. Moneda ideală sau zarul ideal există doar în manualele de teorie a probabilităților. Cu toate acestea, statisticienii vor identifica frecvent un model matematic care să se potrivească, măcar aproximativ, fenomenului pe care îl analizează. Dacă trebuie să previzionăm rezultatul aruncării unei monede din lumea reală, probabil ușor dezechilibrată, va fi necesar să folosim modelul monedei perfect echilibrate. Numim model statistic o simplificare a realității ce permite aproximarea fenomenelor din lumea reală cu ajutorul legilor stocastice. Moneda perfect echilibrată este un astfel de model, investigarea sa în mod pur teoretic informându-ne parțial despre ce se va întâmplă la aruncarea unei monede reale. Deși previzionarea este relativ slabă, și niciun model nu ne va spune precis cum va cădea o monedă reală la următoarea aruncare, legile probabilității vor oferi o idee despre ce se va întâmpla în cursul a mai multor aruncări (“la o mie de aruncări, cca 500 vor fi pajură”), precum și o măsură a incertitudinii din jurul acestei predicții (rareori vor fi precis 500, însă “la repetarea miei de aruncări de multe ori, cca 49% din serii se vor încheia cu 490-510 pajuri”).

De exemplu, nu este nevoie de statistică pentru a calcula înălțimea unui om în metri, dacă o știm pe cea în centimetri. Însă, la descoperirea unei urme de picior de dinozaur, am putea încerca să îi estimăm greutatea, înălțimea etc, pe baza caracteristicilor acelor amprente, și pe baza experienței cu amprente în noroi de la alte animale de înălțime și greutate cunoscute. Modelul statistic va fi probabil o ecuație în care vom folosi proprietățile amprentei de dinozaur și unele numere derivate din greutățile animalelor extante, al cărei rezultat va fi o estimație a greutății acelui dinozaur.

Reversul acestei abordări este modul în care statisticianul trebuie să își descrie produsele. Pe lângă incertitudine previzibilă, măsurabilă, necesitată de aplicarea legilor stocastice, rezultatele analizelor statistice sunt și mai incerte, deoarece ele sunt complet corecte numai pentru modelul statistic (pentru moneda ideală, zarul ideal etc), și doar parțial corecte pentru lumea reală. Dacă mai luăm în calcul și incertitudinile date de erorile de măsurare, de cele de reprezentativitate, de limitările computaționale, etc., devine evident că statisticienii produc aproximări. Mai precis, statisticienii produc legități (propoziții de regulă adevărate), nu legi (propoziții adevărate întotdeauna). Vom spune “rata inflației va fi între 2,0% și 3,2%, cu un nivel de încredere de 95%”, evitând numerele extrem de precise și cuvintele cu caracter definitiv, și incluzând termeni probabilistici, în măsura în care publicul-țintă poate tolera.

Legitățile generate de statistician sunt diferite de legile din fizică, chimie etc, în câteva aspecte. În primul rând, statisticianul este încurajat își descrie produsele în termeni incerți, câtă vreme oferă și o măsură a incertitudinii. Prin contrast, fizicienii doresc ca legile lor să fie precise, deviațiile de la legi invalidând legea. Acum 150 de ani, mii de articole au discutat în contradictoriu pe tema vitezei luminii în apă. Unii fizicieni susțineau că apa “duce” lumina, așa că lumina va călători mai rapid prin apă, dacă apa curge în aceeași direcție. Tabăra opusă susținea că lumina călătorește în eter, o substanță neidentificată, care staționează peste tot în univers. Cei din urmă preconizau că viteza luminii în apă e aceeași, indiferent dacă apa staționează, curge în aceeași direcție cu lumina, sau curge în direcție opusă. Când s-a putut măsura viteza luminii în apă curgătoare, s-a constata că nici unul din modele nu estima corect efectul curgerii apei, lumina mergând ceva mai repede, dar nu cu viteza așteptată, atunci când era “dusă” de apă. Fizicienii epocii au reacționat în primul rând prin a nega rezultatele experimentului, întrucât nu puteau imagina o explicație. Măsurătoarea a fost repetată în variante din ce în ce mai sensibile, deși rezultatele erau mereu între cele două rezultate așteptate. După jumătate de secol, teoria relativității a explicat rezultatul printr-o ecuație mult mai complexă, și folosind o bază teoretică mult mai avansată, moment în care fizicienii au ales să se oprească, în sfârșit, din măsurători.

Un statistician s-ar fi declarat mulțumit dacă ar fi putut enunța o ecuație ce prezice viteza luminii în apă curgătoare, în funcție de viteza apei, chiar și cu unele abateri, cu sau fără explicație, în măsura în care abaterile pot fi și ele estimate cu ajutorul modelului.

Modelele fizicienilor, chimiștilor etc susțin o formă de previziune ce nu lasă loc de abatere. De exemplu, forța ce pune în mișcare un corp cu o anumită accelerație este proporțională cu masa (“greutatea”) corpului, iar măsurătorile care caută eventuale discrepanțe au ajuns deja la a 15 zecimală de precizie. Prin urmare, \(F=ma\) este o certitudine, fără loc de variație. În modelele deterministice, cum este această lege a lui Newton, un set de date de intrare duce întotdeauna la aceleași date de ieșire.

Modelele stocastice sunt întotdeauna nedeterministice, în sensul că includ și o componentă aleatorie. De exemplu, numărul de “capete” de la aruncarea de o mie de ori a unei monede poate fi previzonat numai la modul aproximativ, fiecare set de o mie de încercări ducând la un alt rezultat, la fel de imprevizibil dincolo de faptul că va fi aproximativ 500.

Metodologia statisticii

Modul în care statisticienii își îndeplinesc sarcinile urmează frecvent un șablon, numit metodologie:

1. proiectarea cercetării, adică stipularea unei ipoteze (de exemplu, “bogații cheltuie mai mult decât săracii”, sau, în limbaj tehnic, “veniturile se corelează cu cheltuielile”) și stipularea unei strategii (“vom colecta date despre venituri de la Institutul de Statistică și vom estima cheltuielile din numărul de autovehicule per familie”)
2. observare statistică, adică obținerea datelor în formă brută
3. prelucrarea primară, adică aducerea datelor la o formă ce poate fi procesată statistic
4. modelarea datelor, adică
   • estimarea parametrilor modelului / modelelor
   • unde este cazul, compararea performanțelor modelelor și
   • alegerea modelului optim
5. interpretarea modelului
6. punerea în practică a modelului, care
   • se poate limita la publicarea descoperirii unui efectiv, a unei medii, a unei corelații etc. sau
   • se poate extinde la previzionare, în cazul modelelor de regresie
7. măsurarea eficienței modelului în lumea reală, urmata de eventuala sa rafinare, abandonare sau continua utilizare.

Observarea statistică

Ca regulă, statisticianul nu măsoară direct datele pe care le analizează. Din acest motiv, uneori, colaboratorii însărcinați cu mânuirea eficientă a ruletei și cântarului se referă la statisticieni ca research parasites. Sintagma este mai amuzantă, când notăm că respectivii colaboratori includ în activitatea lor, invariabil, contribuția unor statisticieni înalt specializați, fără ajutorul cărora datele ar rămâne la stadiul de tabel-inventar.

Observarea statistică este deci procesul prin care statisticianul obține datele necesare analizei sau previzionării. Întrucât statisticianul nu operează aparatele de măsură, regulile observării statistice sunt generale. Cea mai importantă regulă este construirea unui plan de observare, care să descrie, pe baza obiectivelor decise în faza de proiectare și înainte de începerea colectării de date

• scopul cercetării
• locul și momentul / intervalul de timp
• care vor fi unitățile statistice, populația, variabilele
• metodele de eșantionare, măsură, stocare etc.

O mnemonică descriind cum ar trebui să fie un plan bun este SMART:

• Specific (cu detalii concrete)
• Measurable (cu rezultate măsurabile)
• Achievable (cu obiective realizabile)
• Relevant (cu rezultate relevante pentru client / organizație)
• Time-bound (încadrate în timp).

În cursul observării, datele se strâng în

• fișe (letrice sau electronice), când punem la un loc informațiile despre o singură unitate statistică, sau
• liste, când descriem la un loc toate unitățile statistice.

În cursul observării, datele se strâng în

• fișe (letrice sau electronice), când punem la un loc informațiile despre o singură unitate statistică, sau
• liste, când descriem la un loc toate unitățile statistice.

Sondaj sau anchetă?

Ancheta de opinie este aplicarea unui chestionar amplu pe un grup de subiecți relativ mic și selectat nealeator. Prin contrast, sondajul este colectarea de date dintr-un eșantion perfect aleator.

În practică, sondajul aleator este mai mult un deziderat decât o procedură realizabilă. În primul rând, tragerea la sorți cu bile, metoda clasică de sondaj complet aleatoriu, devine dificilă când efectivul populației ajunge la mii sau mai mult. În teorie, am putea înlocui tragerea la sorți fizică cu una virtuală, efectuată de calculator, însă așa-zisele numere aleatoare generate de computer sunt de fapt numere din liste foarte lungi, pre-calculate. Mult timp, pentru a se asigra imprevizibilitatea eșantionării, s-au folosit, ca numere cu adevărat aleatoare, duratele de timp dintre emisiile consecutive ale unor specimene radioactive. Și în mileniul 3 puteți cumpăra cărți întregi cu intervalele, în secunde, dintre particulele alfa consecutive emise de o bucată de minereu de uraniu.

Chiar și cu alegeri bazate pe numere realmente aleatoare, selecțiile complet aleatoare (zise selecții probabilistice) devin imposibile când dorim să investigăm populații mari, de ordinul milioanelor, pentru că, în mod normal, nu vom avea acces la lista tuturor membrilor acelei populații. În aceste cazuri, statisticienii vor folosi metode de eșantionare care să permită construirea unui eșantion relativ similar populației de bază, fără a spori exagerat cheltuielile sau timpul necesar studiului.

Panelul este aplicarea consecutiva a aceluiași chestionar pe aceiași subiecți, la intervale de timp regulate.

Monografia statistică este un raport amplu, cu informații din diverse perspective, despre același domeniu economic sau regiune geografică.