Prima intenție a unui analist care este însărcinat să descrie un set de numere, în modul cel mai succint, este să le combine într-un singur număr, preferabil cât mai aproape de fiecare din valorile individuale. În funcție de forma distribuției și de tipul de variabilă, trei astfel de numere îndeplinesc rolul de sumar: media aritmetică și variațiile sale, mediana și valoarea modală. În facultățile cu profil economic, se testează calcularea acestor trei indicatori din serii de date (enumerări de valori), din serii de distribuție pe valori individuale, și din serii de distribuție pe intervale.
Valoarea modală
Valoarea modală (eng. mode) este cea mai comună valoare din seria de date. Valoarea modală este este potrivită majorității cazurilor în care media aritmetică nu este dezirabilă.
- De exemplu, media aritmetică nu se poate calcula pentru variabile calitative, însă este frecvent calculabilă pentru variabile calitative, câtă vreme setul de valori posibile este mic.
- Pe de altă parte, în cazurile în care variabila este cu adevărat continuă, este foarte rară situația în care două unități statistice au aceeași valoare caracteristică (vezi cazul populațiilor orașelor din România, a cohortelor de vărstă etc.). În astfel de cazuri, toate valorile caracteristice vor descrie grupuri de frecvență absolută 1.
Este trivial să calculăm valoarea modală atunci când avem o serie de distribuție pe valori individuale. De fapt, pentru a calcula valoarea modală pentru o listă de valori, va fi necesar să calculăm seria de distribuție. De exemplu, date fiind 2, 10, 10, 10, pentru a calcula valoarea modală sunt necesare:
- calcularea seriei de distribuție, aici N(xᵢ =2) = 1 și N(xᵢ = 10) = 3
- identificarea frecvenței / frecvențelor* maxime, aici 3
- declararea ca valoare modală a tuturor valorilor caracteristice cu această frecvență (aici, Mo = 10).
*Este posibil ca o variabilă să aibă mai multe valori modale.
Problema se rezolvă identic, prin căutarea intervalului cu frecvență maximă, indiferent dacă datele ne parvin ca frecvență absolută sau ca frecvență relativă:
| Notă (variantă statistică, Xᵢ) | Număr de astfel de note (frecvența absolută, Nᵢ) | Note |
| 2 | 1 | |
| 10 | 3 | Cea mai mare frecvență absolută de grup pe valoare unică, corespunzând valorii modale. |
Respectiv:
| Notă (variantă statistică, Xᵢ) | Proporția numărului de astfel de note (frecvența relativă, pᵢ) | Note |
| 2 | 0,25 | |
| 10 | 0,75 | Cea mai mare frecvență relativă de grup pe valoare unică, corespunzând valorii modale. |
Calculul valorii modale pentru serii de distribuție pe intervale
Seria de distribuție a vârstelor cunoscute ale pasagerilor de pe Titanic, pe intervale de decenii, este
| Interval de vârstă | Frecvența absolută a grupei de interval |
| 0 – 9,9 | 62 |
| 10 – 19,9 | 102 |
| 20 – 29,9 | 220 |
| 30 – 39,9 | 167 |
| 40 – 49,9 | 89 |
| 50 – 59,9 | 48 |
| 60 – 69,6 | 19 |
| 70 – 79,9 | 6 |
| cel puțin 80 | 1 |
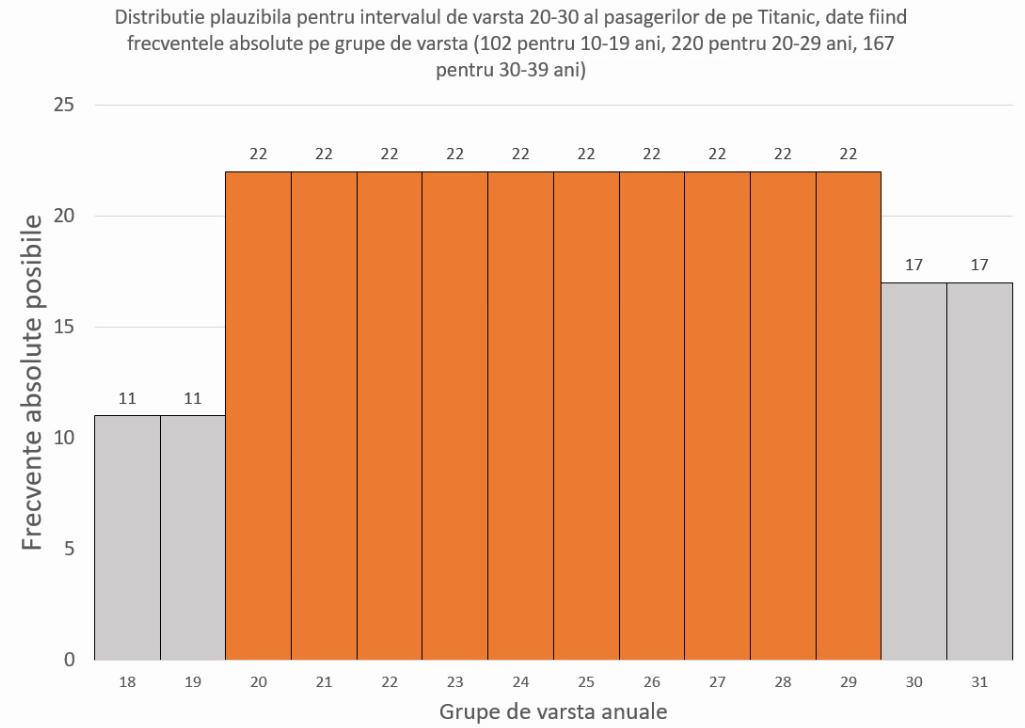
Este evident că cele mai comune vârste sunt cele din intervalul 20-30 ani, însă sarcina va fi de regulă să determinăm o valoare modală precisă, nu un interval. Întrucât pasagerii erau cu precădere imigranți în căutare de lucru, observăm că cei de vârste ale copilăriei (10-20) sunt mai puțini decât cei de 30-40 ani (102, comparat cu 167). În lipsa altor informații, este de presupus că cei 220 de pasageri din intervalul modal vor fi distribuiți în interiorul intervalului modal, pe grupe mai mici (de exemplu, pe ani), într-o manieră similară, asimetrică, cu mai mulți pasageri în partea înaltă a intervalului 20-30:
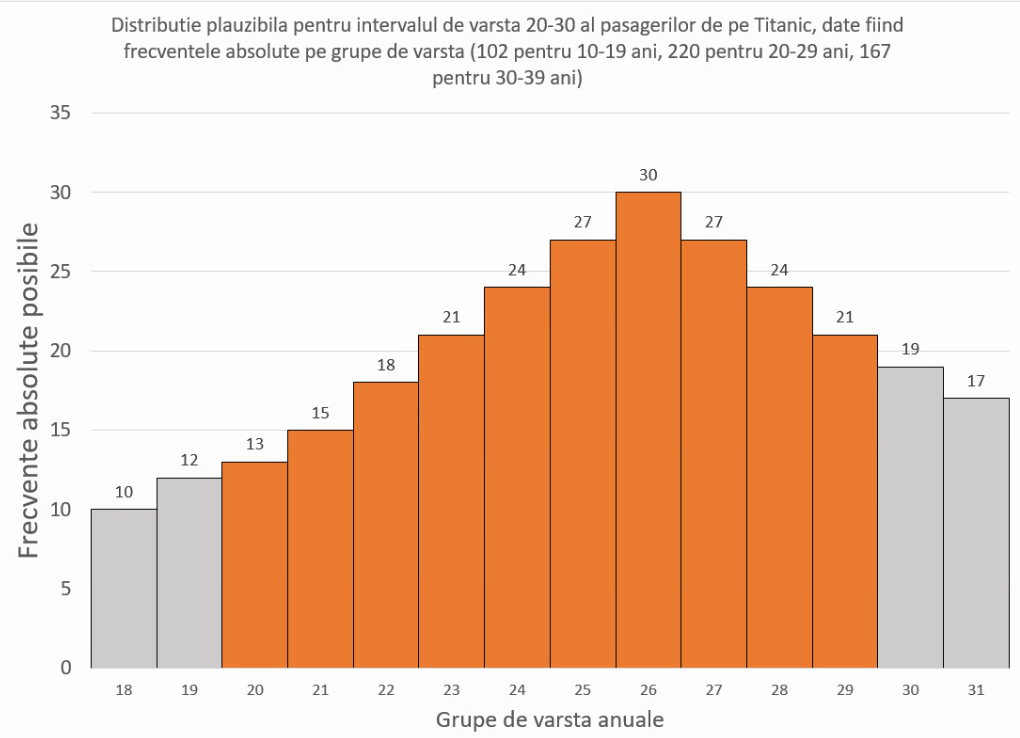
Aceste distribuții propuse se pot transforma din 10 intervale aproximate, ca în imaginea de mai sus, în sute, mii etc., rezultatul rămânând în mare același, respectiv un interval modal asimetric, localizat spre partea inferioară a intervalului 20-30 ani. În cazul în care intervalele propuse pentru interiorul lui 20-30 devin extrem de înguste, linia care va contura toate vârfurile de coloană (adică poligonul frecvențelor va avea forma similară cu cea a liniei punctate roșii:
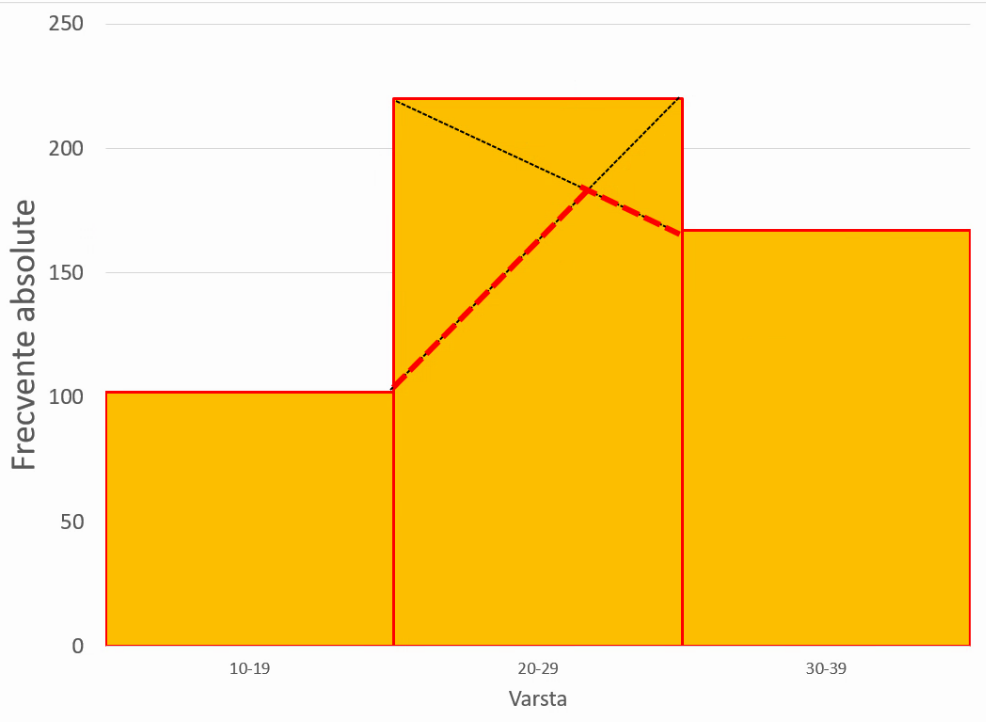
Putem trasa o linie orizontală prin punctul de înălțime maximă (linia verde AB):
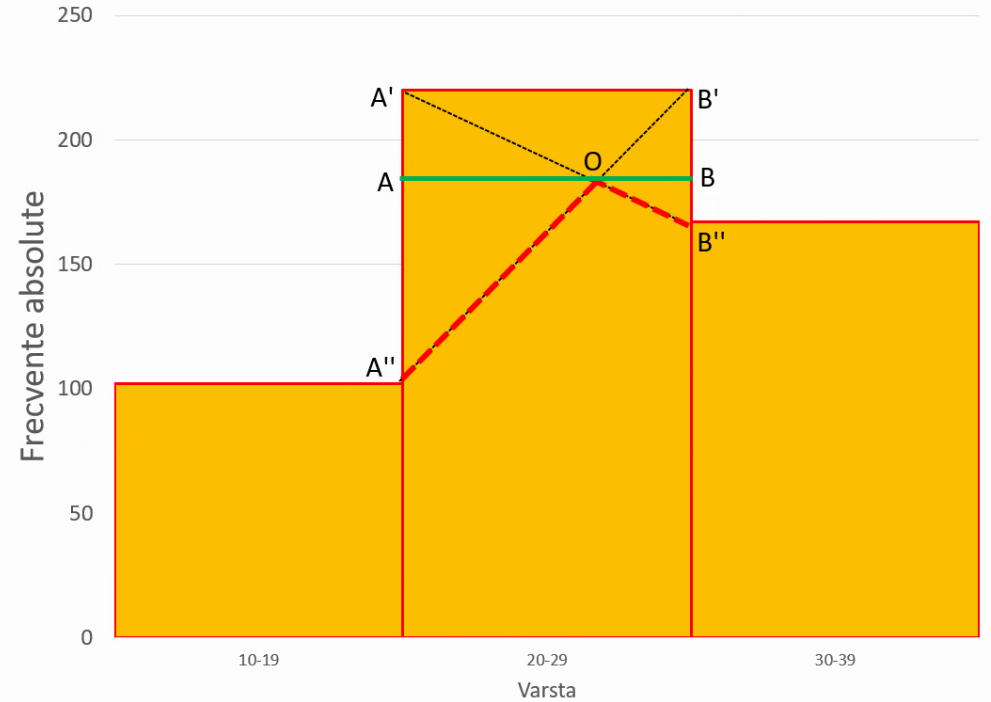
Segmentele AO și BO ne dau distanța de la punctul unde ar trebui să se afle valoarea modală și dreptele verticale ce trec prin cele două margini ale intervalului modal (aici, x=20 și x=30).
- Triunghiurile AOA’ și BOB” sunt asemănătoare, și deci AO / OB = AA’ / BB”. Extragem AA’ = BB” · AO / OB
- Similar, triunghiurile AOA” și BOB’ sunt asemănătoare, și deci AO / BO = AA” / BB’. Extragem AA” = BB’ · AO / OB.
Suma celor două relații, este AA’ + AA” = (BB’ + BB”) · AO / OB. Notăm
- diferența de frecvență Δ₁ reprezentând (frecvența intervalului modal) – (frecvența intervalului premodal), respectiv A’A” în imagine
- diferența de frecvență Δ₂ reprezentând (frecvența intervalului modal) – (frecvența intervalului postmodal), respectiv B’B” în imagine.
Astfel Δ₁ = Δ₂ · AO / OB. Dacă AO/OB = Δ₁ / Δ₂, atunci proporția din lățimea intervalului (aici din 20-30) ocupată de AO este AO/AB = Δ₁ / (Δ₂ + Δ₁). În acest exemplu, poziția valorii modale este probabil între 20 și 30 ani, și mai precis la dreapta axei x=20 cu o distanță AO = AB · Δ₁ / (Δ₂ + Δ₁) = 10 ani · (220-102) / ((220-102) + (220-176)) = 10 ani · 118 / (118 + 53) ≈ 10 ani · 0,69 = 6,9 ani. Deci valoarea modală este probabil 20+6,9 = 26,9 ani.
În mod excepțional, aici dispunem de seria de distribuție la nivel anual:
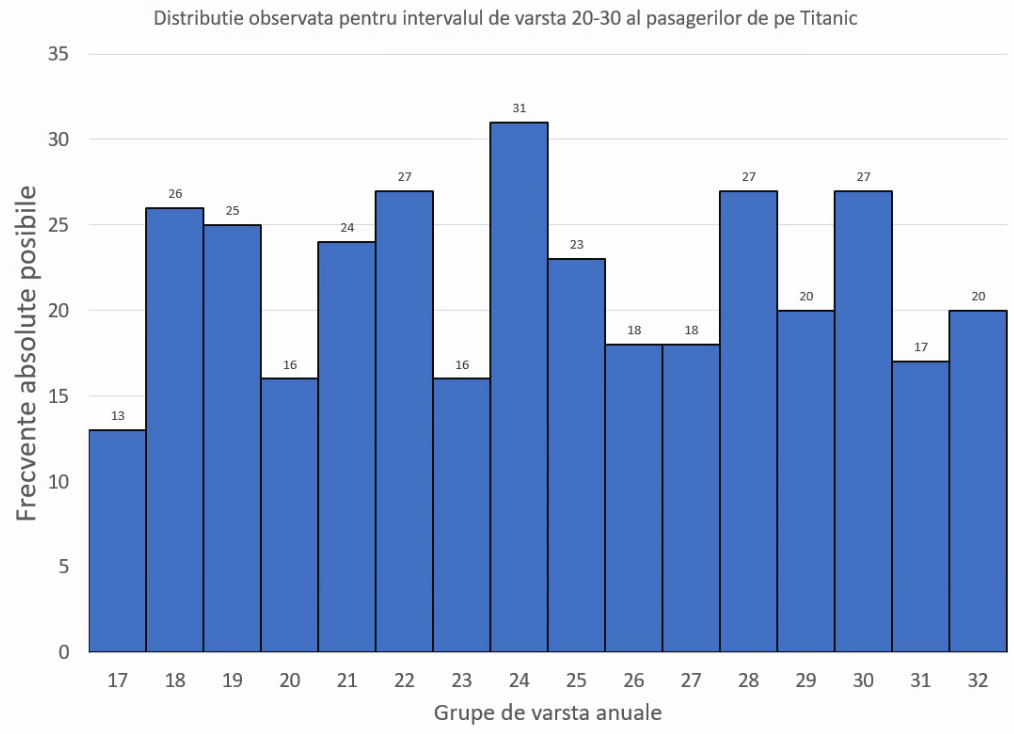
Valoarea modală era în realitate 24 de ani, și distribuția în interiorul intervalului 20-29 ani nu era asemănătoare aproximării sugerate mai sus, demonstrând că metoda Δ₁-Δ₂ este doar o aproximare, mai mult sau mai puțin potrivită situațiilor reale.
Calculele sunt identice în cazul în care seria de distribuție pe intervale este dată cu frecvențe relative. Aici problema ar putea începe cu:
| Interval de vârstă (ani) | Frecvența relativă a grupei de interval |
| 0 – 9 | 0.0868 |
| 10 – 19 | 0.1429 |
| 20 – 29 | 0.3081 |
| 30 – 39 | 0.2339 |
| 40 – 49 | 0.1246 |
| 50 – 59 | 0.0672 |
| 60 – 69 | 0.0266 |
| 70 – 79 | 0.0084 |
| 80 – 89 | 0.0014 |
Aici:
- Identificăm frecvența maximă, aici 0,3081
- Identificăm grupul căreia îi aparține frecvența maximă (grupul modal), aici “20-29 ani” descriind intervalul [20,30).
- Identificăm frecvențele în grupul precedând grupul modal (premodal, aici 0,1429) și în grupul ce urmează grupului modal (postmodal, aici 0,2339)
- Calculăm Δ₁ = frecvențamodal – frecvențapremodal = 0,3081 – 0,1429 = 0,1652 și Δ₂ = frecvențamodal – frecvențapostmodal = 0,3081 – 0,2339 = 0,0742.
- Calculăm proporția din lățimea intervalul modal ocupată de distanța (limită inferioară – valoare modală), adică AO/AB în exemplul de mai sus, cu Δ₁ / (Δ₁ + Δ₂) = 0,1652 / (0,1652+0,0742) = 0,69.
- Calculăm distanța (limită inferioară – valoare modală), adică AO în exemplul de mai sus, folosind rezultatul de mai sus și lăîimea intervalul modal (aici 10 ani), obținând 10 · 0,69 = 6,9 ani
- Calculăm poziția absolută a valorii modale ca fiind suma dintre poziția limitei inferioare (20 ani) și a numărului de mai sus. Deci valoarea modală va fi 20+6,9 = 26,9 ani, ca mai sus.
Pe scurt, valoarea modală este \(Limita_{inf} + (Limita_{sup} – Limita_{inf}) \times \frac{\Delta_1}{\Delta_1 + \Delta_2} \) unde \(\Delta_1 = N_{modal} – N_{premodal} \) și \(\Delta_2 = N_{modal} – N_{postmodal} \)
Mediana și alți indicatori de poziție
În primă instanță, mediana este valoarea care împarte șirul de valori ordonate crescător în două submulțimi de mărime egală.
De exemplu, dată fiind seria de date (4,2,2,7,8) de efectiv 5:
- calculăm modul de partiționare: vom rezerva o valoare pentru mediană, restul fiind partiționat în două submulțimi de efectiv egal, (n-1)/2, aici 2
- ordonăm crescător valorile, obținând șirul cu poziții fixe (2,2,4,7,8)
- identificăm prima submulțime de 2 valori din șirul ordonat, respectiv (2,2)
- identificăm mediana ca valoarea din poziția imediat următoare submulțimii de mai sus, 4, din poziția \( \frac{n-1}{2} + 1 = \frac{n+1}{2}\), aici valoarea din poziția a treia, adică 4.
Aceste calcule sunt înlocuite cu o aproximare, dacă efectivul colectivității este un număr par. Dacă avem de calculat mediana seriei de date (2,9,4,7,8,2) cu n=6 valori:
- calculăm echivalentul poziția medianei, care este tot (n+1)/2, aici 3,5
- ordonăm crescător valorile, obținând șirul cu poziții fixe (2,2,4,7,8,9)
- identificăm vecinii potențialei mediane, aici echivalentul de poziție 3,5 fiind situat între a treia și a patra valoare din șirul ordonat (deci între 4 și 7)
- identificăm mediana ca fiind la jumătatea distanței dintre 4, și 7, adică la (4+7)/2 = 5,5.
Dacă ne este oferită numai seria de distribuție, este necesar să calculăm frecvențele cumulative ascendente pentru a localiza mediana.
În exemplul precedent, am ales mediana la jumătatea distanței dintre 4 și 7 pentru că și echivalentul poziției medianei este la jumătatea distanței dintre poziția a treia și poziția a patra. Într-o altă secțiune discutăm alți indicatori similari mediane, care nu vor arată mijlocul șirului ordonat, ci poziția care separă primul sfert a colectivității de restul etc., scenarii în care “jumătatea distanței dintre două valori” va fi doar unul din multele cazuri posibile.
Calculul medianei pentru serii de distribuție pe valori individuale
Pentru serii de distribuție pe valori individuale, calculele se rezumă la identificarea grupei de valori în care se găsește mediana, ca atare (poziția medianei) sau ca aproximare (echivalentul poziției medianei). De exemplu, să presupunem că o grupă de studenți a luat următoarele note la un examen:
| Notă (variantă statistică, Xᵢ) | Număr de studenți cu această notă (frecvență absolută, Nᵢ) |
| 7 | 2 |
| 8 | 4 |
| 9 | 6 |
| 10 | 2 |
Din nou începem prin a calcula poziția medianei. Avem o colectivitate cu efectiv N = ΣNᵢ = 14. Echivalentul poziției medianei este (N+1)/2 = 7,5.
Pentru a identifica care din cele patru grupe conține mediana, va fi necesar să adăugați frecvențe cumulative ascendente tabelului inițial, folosind convențiile economiștilor (prima frecvența cumulativă ascendentă va fi egală cu prima frecvență de grup, iar celelalte se calculează prin adunări succesive):
| Notă (variantă statistică, Xᵢ) | Număr de studenți cu această notă (frecvență absolută, Nᵢ) | Număr de studenți cu cel puțin această notă (frecvența cumulativă ascendentă) |
| 7 | 2 | 2 |
| 8 | 4 | 2+4 = 6 |
| 9 | 6 | 6+6 = 12 |
| 10 | 2 | 12+2 = 14 |
Studentul cu nota mediană ar fi în echivalentul poziției 7,5 deci
- nu ar putea fi în primul interval de frecvență cumulativă (“cel mult 7”), care cuprinde numai 2 studenți
- nu ar putea fi în al doilea interval de frecvență cumulativă (“cel mult 8”), care cuprinde numai 6 studenți
- ar fi inclus în al treilea interval de frecvență cumulativă (“cel mult 9”), care cuprinde 12 studenți.
Ultimele două propoziții spun că studentul median ar avea cel mult 9, dar nu are cel mult 8 (cu alte cuvinte, are mai mult de 8). Nota mediană este deci 9.
La modul general, o dată calculate frecvențele absolute, sarcina voastră este să identificați cel mai îngustă clasă de frecvență cumulativă care are frecvența mai mare decât poziția medianei. Diferența între această clasă (“cel mult 9”) și clasa vecină mai limitată (“cel mult 8”) este chiar grupul definit de valoarea medianei (“precis 8”).
Dacă seria de distribuție pe valori individuale este dată cu frecvențe relative, se repetă pasul de calculare al frecvenței cumulative ascendente și cel de căutare al poziției medianei, cu singura schimbare că poziția medianei în lista frecvențelor relative va fi 0,5. De exemplu, pentru o altă colectivitate de studenți, am putea avea următoarea distribuție:
| Notă (variantă statistică, Xᵢ) | Proporție de studenți cu această notă (frecvență relativă, pᵢ) |
| 6 | 0,1 |
| 7 | 0,2 |
| 8 | 0,25 |
| 9 | 0,25 |
| 10 | 0,3 |
Calculăm frecvențele relative cumulative ascendente:
| Notă (variantă statistică, Xᵢ) | Proporția de studenți cu această notă (frecvență relativă, pᵢ) | Proporția de studenți cu cel puțin această notă (frecvență relativă cumulativă ascendentă) |
| 6 | 0,1 | 0,1 |
| 7 | 0,2 | 0,1+0,2 = 0,3 |
| 8 | 0,25 | 0,3+0,25 = 0,55 |
| 9 | 0,25 | 0,55+0,25 = 0,8 |
| 10 | 0,2 | 0,8+0,2 = 1 |
Identificăm cel mai îngust interval de frecvență cumulativă care conține echivalentul de poziție al medianei. Aici, 0,5 ar fi cuprins in clasa “cel puțin 8”, dar nu va fi inclus în grupul “cel puțin 7”. Deci mediana este în diferența celor două clase, respectiv în grupul definit de nota 8. Mediana va fi 8.
Calculul medianei pentru serie de distribuție pe intervale
În acest caz, primii pași sunt identici, constând în calcularea echivalentului poziției medianei și a frecvențelor cumulative ascendente și identificarea cele mai înguste clase de frecvență cumulativă ascendentă care include și poziția medianei. Revenind la exemplul pasagerilor de pe Titanic, putem porni de la seria de distribuție pe intervale de mai sus:
| Interval de vârstă | Frecvența absolută a grupei de interval |
| 0 – 9,9 | 62 |
| 10 – 19,9 | 102 |
| 20 – 29,9 | 220 |
| 30 – 39,9 | 167 |
| 40 – 49,9 | 89 |
| 50 – 59,9 | 48 |
| 60 – 69,6 | 19 |
| 70 – 79,9 | 6 |
| cel puțin 80 | 1 |
Efectivul colectivității este 714, deci echivalentul poziției medianei este (714+1)/2 = 357,5. Adăugăm frecvențele cumulative ascendente, în convenția economiștilor (adică frecvențele clasei celei mai înguste care include și grupul de pe acea linie):
| Interval de vârstă | Frecvența absolută a grupei de interval | Frecvență absolută cumulativă ascendentă |
| 0 – 9,9 | 62 | 62 |
| 10 – 19,9 | 102 | 164 |
| 20 – 29,9 | 220 | 384 |
| 30 – 39,9 | 167 | 551 |
| 40 – 49,9 | 89 | 640 |
| 50 – 59,9 | 48 | 688 |
| 60 – 69,6 | 19 | 707 |
| 70 – 79,9 | 6 | 713 |
| cel puțin 80 | 1 | 714 |
Prin compararea acestor frecvențe cu echivalentul poziției medianei (357,5), aflăm că cel mai îngust interval care cuprinde mediana este (-∞, 30) ani, iar cel mai vast interval care nu cuprinde mediana este (-∞,20) ani. Prin urmare, intervalul ce conține mediana este [20,30).
Pentru a identifica mai precis o valoare a medianei vom face o presupunere diferită de cea de mai sus, una în care vom presupune că distribuția în interiorul fiecărui interval este uniformă:
În această ipoteză, se presupune că avem un număr egal de pasageri în fiecare grup de interval anual de vârstă, dar și în fiecare grup lunar, zilnic etc., putând duce detaliile la infinit și trata vârsta ca o variabilă continuă.
Trebuie să identificăm poziția pe axa continuă a vârstelor care îi partiționează pe cei 220 de pasageri din grupul valorii mediane în două submulțimi, mai tineri decât mediana și mai bătrîni decât mediana. Conform serie de distribuție, prima persoană din grupul medianei are poziția 165 în șirul ordonat a vârstelor, iar ultima are poziția 384, și deci sarcina noastră este să identificăm acea vârstă care îî partiționează pe cei 220 în:
- 357-165 + 1* = 193 mai tineri decât mediana
- 384-358 + 1* = 27 mai bătrâni decât mediana.
* Adăugarea lui 1 este necesară pentru că așa funcționează diferențele de ranguri. Între al doilea și al patrulea număr nu avem 4-2 = 2 numere, ci cu unul mai mult. La valori mari ale frecvențelor relative, se practică o aproximare care ignoră această corecție, pe care o voi face .
În distribuția uniformă, această valoare se afla într-un punct al cărui distanțe până la margini sunt proporționale cu frecvențele din cele două submulțimi. Aici ariile dreptunghiurilor AOO’A” și BOO’B’Ț’ ar trebuii să fie proporționale cu rangmediana – ranginferior ≈ 193 și respectiv rangsuperior – rangmediana ≈ 27.
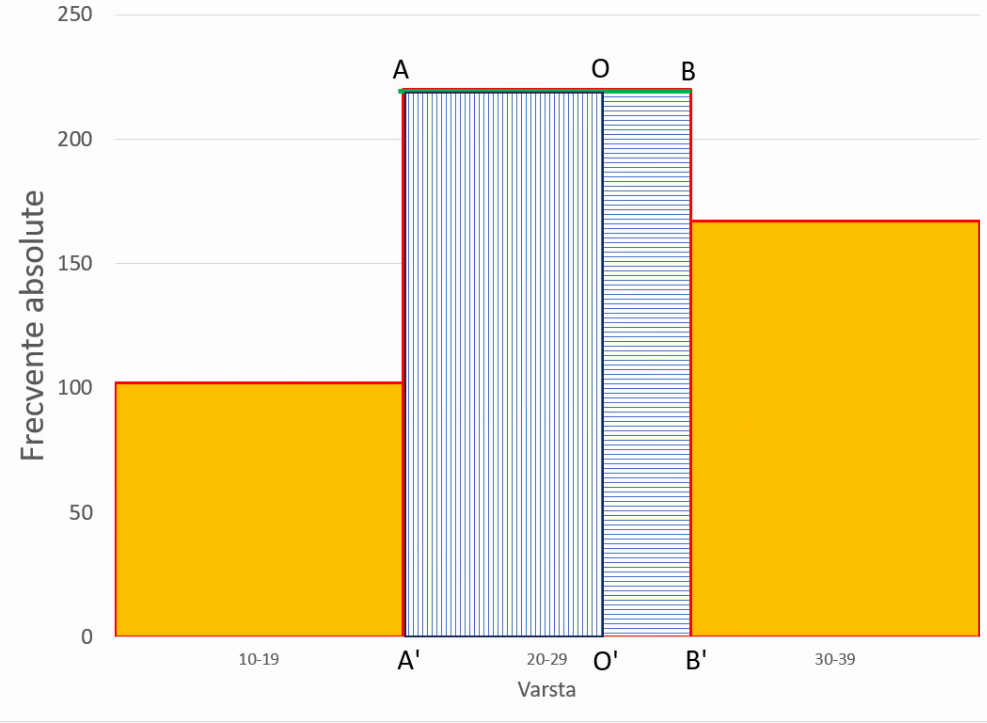
Dreptunghiurile având aceeași lungime, vom scrie că și raportul lățimilor BO/AO este egal cu (rangsuperior – rangmediana) / (rangmediana – ranginferior) = 27/193. Adunăm 1 la ambele rapoarte, obținând pe de o parte 1 + (BO/AO) = (AO/AO) +(BO/AO) = AB/AO, și pe cealaltă 1 + (rangsuperior – rangmediana) / (rangmediana – ranginferior) = (rangsuperior – rangmediana + rangmediana – ranginferior) / (rangmediana – ranginferior) = (rangsuperior – ranginferior) / (rangmediana – ranginferior), aici 220/193.
Cum rangsuperior – ranginferior este frecvența absolută în intervalul medianei, scriem AB/AO = Nmedian / (ranginferior – rangmediana). Deci AO, distanța d ela marginea inferioară a interbvalului median la valoarea cea mia probabilă a medianei este (Lățimea intervalului median în ani) * (rangmediana – ranginferior) / Nmedian, aici 10 ani · (357,5 – 164) / 220 = 10 ani · 0,878 = 8,78 ani. Mediana va fi cel mai probabil 20 + 8,78 = 28,78 ani.
Pentru o serie de distribuție pe intervale cu frecvențe relative, vom aplica același procedeu, cu singura modificare fiind echivalentul poziției medianei de 0,5. De exemplu, dată fiind această serie de distribuție:
| Interval de vârstă (ani) | Frecvența relativă a grupei de interval |
| 0 – 9 | 0.0868 |
| 10 – 19 | 0.1429 |
| 20 – 29 | 0.3081 |
| 30 – 39 | 0.2339 |
| 40 – 49 | 0.1246 |
| 50 – 59 | 0.0672 |
| 60 – 69 | 0.0266 |
| 70 – 79 | 0.0084 |
| 80 – 89 | 0.0014 |
Vom începe prin a calcula frecvențele cumulative ascendente:
| Interval de vârstă (ani) | Frecvența relativă a grupei de interval | Frecvența relativă cumulativă ascendentă |
| 0 – 9 | 0.0868 | 0,0868 |
| 10 – 19 | 0.1429 | 0,2297 |
| 20 – 29 | 0.3081 | 0,5378 |
| 30 – 39 | 0.2339 | 0,7717 |
| 40 – 49 | 0.1246 | 0,8964 |
| 50 – 59 | 0.0672 | 0,9636 |
| 60 – 69 | 0.0266 | 0,9902 |
| 70 – 79 | 0.0084 | 0,9986 |
| 80 – 89 | 0.0014 | 1 |
Identificăm prima clasă cu frecvență cumulativă ascendentă mai mare decât echivalentul poziției medianei (aici, (-∞,30) ani, cu frecvența cumulativă 0,5378). Întrucât (-∞,20) ani nu conține mediana, vom identifica grupul media ca fiind [20,30) ani, care are frecvență relativă 0,3081.
Pentru a estima poziția cea mai probabilă în interiorul acestui interval, vom calcula proporția din acesta rezervată segmentului (limită inferioară – mediană), AO din imagine, din lățimea intervalului (AB), cu (rangmediana – ranginferior) / pmedian = (0,5 – 0,2297) / 0,3081 ≈ 0,878. Deci segmentului (limită inferioară – mediană) îi revin 10 ani · 0,878 = 8,78 ani. Spune că cea mai probabilă valoare a medianei este 28,78 ani.
Pe scurt, pornind de la o serie de distribuții pe interval, valoarea cea mai probabilă a oricărui indicator pozițional de la poziția P necesită identificarea intervalului de grup în care acesta se află, ca limite inferioară și superioară în termeni variabilei (aici, în ani). Din tabel vom mai prelua frecvenței acestui grup F și frecvența cumulativă ascendentă trecută în dreptul intervalului ce o precede G. Valoarea indicatorului va fi \( Limita_{inf} + (Limita_{sup} – Limita_{inf}) \frac{P-G}{F} \).
- Dacă frecvențele din seria de distribuție, G și F, sunt absolute, P pentru mediană este (n+1)/2, unde n este efectivul colectivității.
- Dacă frecvențele din seria de distribuție, G și F, sunt relative, P pentru mediană este 0,5.
Media aritmetică
Media aritmetică este raportul dintre suma valorilor unei variabile cantitative (totalul colectivității) și numărul lor (efectivul colectivității) \(\frac {\sum_{i=1}^N{x_i}}{N}\). Media aritmetică a eșantionului \( \overline x \)este cel mai bun estimator al mediei aritmetice a populației \( \mu \).
- Dacă, în locul seriei de date \( (x_i) \) cunoaștem doar seria de distribuție pe valori individuale cu frecvențe absolute \(x_j, N_j)\), putem să calculăm suma de la numărătorul formulei precedente cu \( \sum_{j=1}^m{x_j N_j} \), unde m este numărul de grupe. De exemplu, suma a unei note 2 și trei note de 10 este prin definiție 2+10+10+10+10, dar poate fi calculată cu 1·2 + 3·10, media aritmetică fiind, în ambele cazuri, \(32 \over 4\). Cea de-a doua variantă devine practic obligatorie când seria de date are milioane de unități statistice, dar numai câteva valori posibile.
- Această alternativă se va scrie pentru populație \( \mu = \frac{\sum_{j=1}^m{x_j N_j}}{\sum_{j=1}^m{N_j}} \), dat fiind că efectivul populației este \( N = \sum_{j=1}^m{N_j} \).
- În convenția în care efectivele de eșantion se notează cu literă mică, pentru media aritmetică a eșantionului vom scrie aceeași formulă, dar cu notații ajustate: \( \overline X = \frac{\sum_{j=1}^m{x_j n_j}}{\sum_{j=1}^m{n_j}} \).
- O altă variantă a expresiei precedente este cea folosită în cazul seriilor de distribuție pe valori individuale cu frecvențe relative \(x_j, p_j)\), caz în care media aritmetică a populației devine \( \mu = \sum_{j=1}^m{x_j N_j} \). În exemplul de mai sus, proporțiile notelor de 2 și 10 erau 0,25 și 0,75, deci media aritmetică se poate calcula cu 0,25·2 + 0,75·10 = 8.
- Pentru mediile aritmetice ale datelor care ne parvin doar ca serii de distribuție pe intervale de valori, va fi estimat, pentru fiecare grup, o valoare unică care să le reprezinte, folosind metoda centrului de interval. Acea valoare unică va fi folosită în locul lui \( x_j \) din formulele de mai jos.
Media aritmetică este preferată în majoritatea cazurilor când trebuie să descriem tendința centrală.
Denumim abatere (eng. deviation) distanța de la un număr C la o valoare individuală, \(d_{x_i} = x_i – C \). Prin urmare, în raport cu un C, fiecare valoare caracteristică va avea o abatere. În exemplul de mai sus, nota 2 se abate de la media aritmetică 8 cu o abatere 2-8 = -6, iar fiecare din notele de 10 are abatere 10-8 = 2. Media aritmetică este singura măsură a tendinței centrale cu proprietatea că suma abaterilor este 0. Mai mult, suma pătratelor abaterilor (aici (-6)² + 2² + 2² + 2² = 48) este minimă atunci când C este media aritmetică, comparat cu orice alt număr real. Din aceste motive, cuvântul “abatere” fără mențiunea “de la X” este interpretat de statisticieni ca abatere de la media aritmetică.
Media aritmetică este singura măsură a tendinței centrale care poate fi compusă prin combinații liniare. Dacă avem mai multe variabile măsurând același tip de variabilă, \( (x_i) \), \( (y_i) \), \( (z_i) \), etc. cu același număr de valori n, putem folosi orice constante reale, a, b, c etc, pentru a construi, prin combinație liniară, o nouă variabilă \(Q_i = a \times x_i + b \times y_i + c \times z_i + \dots \), iar media aritmetică a noii variabile va fi combinația liniară a mediilor \( \overline Q = a \times \overline x + b \times \overline y + c \times \overline z + \dots \). De exemplu, să presupunem că avem variabilele cu același număr de valori “notă la seminar” și “notă la curs”:
| Student | Nota la seminar | Nota la examen final |
| Robert | 8 | 5 |
| George | 7 | 6 |
| Maria | 8 | 5 |
| Ioana | 5 | 2 |
Media notelor la seminar este 7, iar cea a notelor la examenul final este 4,5. Dacă nota din catalog se calculează prin combinația liniară \(0,3 \times Nota_{seminar} + 0,7 \times Nota_{final}\), nu este necesară calcularea notelor din catalog la fiecare student, pentru a obține media aritmetică a notelor din catalog. Proprietatea de combinare liniară a mediilor aritmetice indică direct media notelor din catalog ca fiind \(0,3 \times \overline {Nota_{seminar}} + 0,7 \times \overline {Nota_{final}}\), adică 0,3·7 + 0,7·4,5.
Această proprietate este folosită frecvent când creăm o nouă variabilă prin înmulțirea cu o constantă. De exemplu, dacă cunoaște înălțimea medie a unui grup de persoane în metri, nu este necesar să cunoaștem valori individuale pentru a calcula înălțimea medie în centimetri. Așa cum fiecare valoare caracteristică din noua serie de date “înălțime în centimetri” este 100 · “înălțimea în metri”, și media aritmetică a “înălțimilor în centimetri” este 100 · media variabilei (“înălțimea în metri”.
Mai folosim abilitatea de a urma combinații liniare a unei variabile atunci când creăm variabile noi prin însumarea pe perechi a unor valori preexistente. Dacă avem seriile \( (x_i) \) și \( (y_i) \), și definim \(z_i = x_i + y_i \), suntem într-un caz particular al formulei de mai sus în care a=b=1, și deci \( \overline {z} = \overline {x} + \overline {y} \).
Este necesar să nu confundați suma cu produsul în exemplul de mai sus. Dacă definim o variabilă \( a_i = x_i y_i \), media noii variabile nu va fi egală cu produsul mediilor seriilor inițiale decât în cazuri foarte rare. De exemplu:
| xᵢ | yᵢ | aᵢ= xᵢyᵢ |
| 0 | 1 | 0 |
| 2 | 3 | 6 |
| 3 | 4 | 12 |
| 3 | 5 | 15 |
| 4 | 5 | 20 |
| 6 | 6 | 36 |
În acest exemplu, mediile sunt \( \overline x = 3 \), \( \overline y = 4 \), \( \overline a = 14,8 \), și deci \( \overline x \times \overline y \neq \overline {xy} \).
Revenind la exemplul pasagerilor de pe Titanic cu vârstă precizată, distribuția vârstelor lor este reprezentată de următoarea histogramă:

Media de ordin k
Numim medie de ordin k numărul m₍ₖ₎ cu proprietatea \( m^k_{(k)} \times N = \sum_{i=1}{N} {x_i^k} \).
Cazul cel mai simplu, unde k = 1, este cel al mediei aritmetice, unde \( \overline{x}^1 \times N = \sum_{i=1}^{N} {x_i^1} \).
Două medii de ordin k sunt folosite atunci când media aritmetică nu surprinde cel mai bine tendința centrală:
- Media pătratică Mₚ este media de ordin 2, deci numărul cu proprietatea \( M_p^2 \times N = \sum_{i=1}^{N} {x_i^2} \). De exemplu, media pătratică a notelor de mai sus este numărul cu proprietatea \( M_p^2 \times 4 = 2^2 + 10^2 + 10^2 + 10^2 \). Ca orice medie de ordin k, se pot folosi variantele din serii de distribuție
- pentru frecvențe absolute, \( M_p^2 \times 4 = 1 \times 2^2 + 3 \times 10^2 \)
- pentru frecvențe relative, împărțind ambii termeni ai egalității de mai sus la N, \( M_p^2 = 0,25 \times 2^2 + 0,75 \times 10^2 \).
- Media armonică Mₕ este media de ordin -1, deci numărul cu proprietatea \( M_h^{-1} \times N = \sum_{i=1}^{N} {x_i^{-1}} \). De exemplu, media pătratică a notelor de mai sus este numărul cu proprietatea \( M_h^{-1} \times 4 = 2^{-1} + 10^{-1} + 10^{-1} + 10^{-1} \).
Mediile de ordin k sunt într-o relație crescătoare cu k, pentru același set de numere \( M_h \leq \overline X \leq M_p \). Spunem că media pătratică acordă importanță sporită valorilor mari comparat cu media aritmetică, iar media armonică acordă importanță mai redusă valorilor mari comparat cu media aritmetică.
Nu există medie de ordin 0, însă, în șirul de mai sus, putem insera în locul acesteia media geometrică, cel mai succint definită ca numărul cu proprietatea că logaritmul său este media aritmetică a logaritmilor valorilor individuale, \( N \times \log M_g = \sum_{i=1}^{N} {\log x_i} \). Deci \( M_h \leq M_g \leq \overline X \leq M_p \).
