Datele statistice sunt mărimi concrete, măsurabile, despre unități statistice, eșantioane sau populații, sau despre grupuri / clase. Ordonarea, gruparea și clasificarea sunt procedee prin care datele statistice sunt sistematizate, proces ce facilitează prezentarea lor în forme ușor de înțeles, ca tabelul de sumar, sau graficul.
Grupare
Populațiile mari prezintă o provocare pentru statistician. Pe de o parte, nu este necesar să le descriem pe larg, cu menționarea fiecărui element, multe din proprietățile populației fiind surprinse de un singur număr (efectiv, total, medie etc). Pe de altă parte, astfel de descrieri cu un singur număr nu pot comunica diversitatea din acea populație. O soluție de compromis este împărțirea populației în câteva submulțimi și descrierea acestora.
Să considerăm colectivitatea județelor din România, cu variabila nominală de bază “Nume”. Pentru următoarele calcule, vom adăuga o a doua variabilă nominală, descriind care dintre cele trei regiuni istorice conține majoritatea respectivului județ:
| Județ | Regiune |
| Alba | Transilvania |
| Arad | Transilvania |
| Argeș | Țara Românească |
| Bacău | Moldova |
| Bihor | Transilvania |
| Botoșani | Moldova |
| Brăila | Țara Românească |
| Brașov | Transilvania |
| București | Țara Românească |
| Buzău | Țara Românească |
| Călărași | Țara Românească |
| Caraș-Severin | Țara Românească |
| Cluj | Transilvania |
| Constanța | Țara Românească |
| Covasna | Transilvania |
| Dâmbovița | Țara Românească |
| Dolj | Țara Românească |
| Gorj | Țara Românească |
| Galați | Moldova |
| Harghita | Transilvania |
| Hunedoara | Transilvania |
| Iași | Moldova |
| Ialomița | Țara Românească |
| Ilfov | Țara Românească |
| Maramureș | Transilvania |
| Mehedinți | Țara Românească |
| Mureș | Transilvania |
| Neamț | Moldova |
| Olt | Țara Românească |
| Prahova | Țara Românească |
| Sălaj | Transilvania |
| Sibiu | Transilvania |
| Suceava | Moldova |
| Timiș | Transilvania |
| Teleorman | Țara Românească |
| Tulcea | Țara Românească |
| Vâlcea | Țara Românească |
| Vaslui | Moldova |
| Vrancea | Moldova |
Fiecare din coloanele tabelului de mai sus este un ansamblu de valori caracteristice, detaliat pentru fiecare unitate statistice, ceea ce se mai numește serie de date, serie statistică, repartiție statistică, sau vector de valori caracteristice.
Putem sumariza această informație cu tabelul:
| Grupă | Județe |
| Moldova | BT, SV, NT, IS, VS, BC, GL, VN, BR |
| Transilvania | BV, SB, AB, HD, AR, BH, CJ, MS, BN, HR, CV, SJ, SM, MM, TM |
| Țara Românească | TL, CT, IL, CL, BZ, PH, B, IF, GR, DB, TL, AG, VL, OT, DJ, GJ, MH, CS |
În cel mai bun caz, cel de-al doilea tabel ar avea ca variabilă nominală șiruri alfanumerice, precum “BT, SV, NT, IS, VS, BC, GL, VN, BR”. În niciun caz nu vom spune că unitatea statistică Moldova are 9 valori caracteristice ale variabilei Județe, variabila având întotdeauna precis o valoare pentru fiecare unitate statistică. În concluzie, tabelul acesta este relativ inutil pentru prelucrări numerice.
Cu toate acestea, sistematizarea informației din acel tabel este informativă, demonstrând că unitățile statistice pot fi organizate în trei submulțimi, unele mai vaste decât altele. Există multe feluri de a organiza submulțimi ale unei colectivități, însă cea de mai sus se remarcă prin modul aparte în care au fost create.
Gruparea (zisă și stratificare) este procedura de prelucrare primară, prin care se descriu submulțimi (“grupe”) a unei populații sau a unui eșantion, astfel încât:
- să nu rămână unități statistice în afara submulțimilor (regula universalității)
- să nu încadreze unități statistice în mai mult de o submulțime (regula unicității).
Se subînțelege că gruparea, similar unității statistice, populației etc, nu se definește ambiguu. Fiecare unitate statistică va trebui să fie alocată clar unei regiuni. Dacă definițiile grupelor lasă loc de ambiguități, este necesară reformularea criteriilor de grupare.
Se recomandă ca gruparea să se facă pe criterii logice, așa încât să putem descrie grupele în mod analitic (prin enunțarea principiilor de grupare ca propoziții, nu ca enumerări). Cu alte cuvinte, este de dorit ca membrii fiecărei grupe să se asemene dintr-un anumit punct de vedere.
Revenind la tabel, numărul de elemente ale submulțimilor este un efectiv (număr cardinal), iar utilizarea lui transformă tabelul în echivalentul unei serii de date.
| Grupa i | Județe | Efectivul grupei, Nᵢ |
| Moldova | BT, SV, NT, IS, VS, BC, GL, VN, BR | 9 |
| Transilvania | BV, SB, AB, HD, AR, BH, CJ, MS, BN, HR, CV, SJ, SM, MM, TM | 15 |
| Țara Românească | TL, CT, IL, CL, BZ, PH, B, IF, GR, DB, TL, AG, VL, OT, DJ, GJ, MH, CS | 18 |
Reamintim că variabila este o funcție care lega fiecare unitate statistică de o valoare caracteristică (aici, R:{Mulțimea județelor} → {Mulțimea regiunilor}). Seria de date este lista valorilor acelei funcții pentru fiecare din unitățile statistice existente. Seria de date este echivalentul imaginii funcției variabilă, cu deosebirea este că, tehnic, o imagine este o mulțime, fără ordine, dar, în seria de date, fiecare element are echivalentul unei poziții. Tehnic, aici, imaginea ar fi mulțimea cu trei elemente {“Moldova”, “Transilvania”, “Țara Românească”}, dar seria de date are 42 de elemente, (R[“Alba”], R[“Arad”], … , R[“Zalău”]), fiecare element având un index. Indexul este similar unei poziții, dar nu dictează o ordine nume.
Prin contrast, cel mai recent tabel descrie valorile unei alte funcții care leagă fiecare grupă de un număr natural (aici, \(N:{Mulțimea\ regiunilor} \rightarrow \mathbb{N} \), cu exemplul N[“Moldova”] = 9). Un ansamblu de valori numerice care prezintă structura unei populații, descriind fiecare grupă, se numește serie de distribuție. Tabelul ce prezintă structurat o serie de distribuție cu cel puțin două coloane, una pentru descriere grupei și una pentru mărimea ei, se numește tabel de distribuție. Funcțiile de forma \(n:{Mulțime\ de\ grupe} \rightarrow \mathbb{R} \) care descriu structura unei colectivități se numesc funcții de distribuție.
Așa cum seria de date este cel mai frecvent tabelată cu fiecare unitate statistică pe o linie, tabelul seriei de distribuție prezintă pe fiecare linie câte o grupă. (Deoarece grupele sunt mai puține decât unitățile statistice, este posibil scenariul alternativ în care fiecărei grupe să i se aloce o coloană.) În afară de prezentarea sub formă de tabel de distribuție, seria de distribuție mai este prezentată ca:
- enumerare ordonată a valorilor, aici (9, 15, 18), însoțită de enumerarea în aceeași ordine a identificatorilor (“Moldova”, “Transilvania”, “Țara Românească”)
- enumerare de perechi (frecvență, descrierea grupei), ca în ((9, “Moldova”), (15, “Transilvania”), (18, “Țara Românească”).
Seria fiind un concept, tabelul și înșiruirile cu paranteze rotunde sunt doar opțiuni de prezentare, la fel de informative.
La fel ca în seria de date, când vom descrie la modul general, în limbaj matematic, relații privind grupele, vom folosi notații care sunt mai corecte pentru șiruri. De exemplu, despre frecvențele relative vom scrie că suma tuturor efectivelor de grupă este egală cu efectivul colectivității
- la modul general, ΣNᵢ = N
- la cazul județelor, unde indecșii nu sunt de fapt numere, NMoldova + NTransilvania + NȚaraRomânească = NRomânia.
Numerele naturale din seria de distribuție de mai sus sunt frecvențe absolute (vezi capitolul Glosarul statisticii). Pe lângă acestea, pentru orice grupare putem defini și o serie de distribuție cu frecvențe relative la efectivul populației. În exemplul nostru, 9 județe din cele 42 sunt în Moldova, deci vom spune că
- frecvența absolută a grupei Moldova este efectivul grupei (numărul cardinal), adică 9
- frecvența relativă a grupei Moldova este proporția grupei în întreaga colectivitate, adică 9/42 ≈ 0,21.
| Grupă | Frecvența absolută, Nᵢ | Frecvență relativă, nᵢ = Nᵢ / ΣNᵢ |
| Moldova | 9 | 9 / 42 ≈ 0,21 |
| Transilvania | 15 | 15 / 42 ≈ 0,36 |
| Țara Românească | 18 | 18 / 42 ≈ 0,42 |
În contextul proporțiilor din întreg, aceste frecvențe relative sunt numere cuprinse între 0 și 1. Frecvențele absolute pot fi 0 sau 1, dar de regulă sunt numere naturale mai mari.
În comunicarea cu publicul, se folosește faptul că semnul % este abrevierea lui “înmulțit cu 1/100”, motiv pentru care veți vedea frecvența relativă a grupului Moldova ca fiind cca 21%. Unele manuale numesc rescrierea unei frecvențe relative sub formă de procent drept frecvență relativă procentuală, și chiar o notează diferit:
| Grupă | Frecvența absolută, Nᵢ | Frecvență relativă, nᵢ = Nᵢ / ΣNᵢ | Frecvență relativă procentuală, nᵢ% = (nᵢ · 100)% |
| Moldova | 9 | 9 / 42 ≈ 0,21 | (0,21 × 100)%, adică 21% |
| Transilvania | 15 | 15 / 42 ≈ 0,36 | (0,36 × 100)%, adică 36% |
| Țara Românească | 18 | 18 / 42 ≈ 0,42 | (0,42 × 100)%, adică 42% |
Dacă gruparea a fost conform regulilor și toate grupele sunt luate în calcul, suma frecvențelor relative este 1, respectiv 100% dacă se folosește forma lor procentuală.
Numerele din tripletul de frecvențe absolute, aici (9, 15, 18), au aceleași relații de proporționalitate între ele ca în tripletul de frecvențe relative (0,21; 0,36; 0,42). De exemplu, ultimul e de două ori mai mare decât primul. Multe alte triplete cu aceste relații de proporționalitate se pot calcula, însă cele maui utile sunt cele generate prin împărțirea frecvențelor absolute la cmmdc (aici, 3), ceea ce produce seria de distribuție cu frecvențe reduse.
| Grupă | Frecvența absolută, Nᵢ | Frecvența redusă, Nᵢ/cmmdcc |
| Moldova | 9 | 9 / cmmdc = 3 |
| Transilvania | 15 | 15 / cmmdc = 5 |
| Țara Românească | 18 | 18 / cmmdc = 6 |
Aceste numere simple sunt foarte utile în comunicarea cu publicul larg. De exemplu, este foarte uțor de înțeles că la fiecare 3 județe din Moldova românească, corespund 6+5 = 11 județe în restul țării.
Clasificare
Clasificarea (agregare) este procedura de prelucrare primară, prin care se descriu reuniuni de grupe, asamblate pe criterii logice, numite clase. În cadrul unei clasificări, o grupă nu poate aparține mai multor clase, și nicio grupă nu este lăsata în afara claselor.
Frecvența unei clase se definește la fel ca la grupe: frecvența absolută va fi numărul cardinal al clasei, iar frecvența relativă va arăta proporția din colectivitate care corespunde acelei clase. Însă frecvența unei clase se poate calcula și ca sumă a frecvențelor grupelor ce o compun.
| Clasă de județe | Frecvența absolută | Frecvența relativă | Frecvență relativă procentuală |
| Ocupație preponderent turcă (Moldova și Țara Românească) | se pot număra; sau se poate calcula suma 9+15 = 27 | din definiție, 27/42 ≈ 0,57; sau calculată ca sumă 0,21 + 0,36 = 0,57 | din definiție, (0,57 × 100)%; sau calculată ca sumă 21% + 36% = 57% |
| Ocupație preponderent austriacă (Transilvania) | 18 | 18/42 ≈ 0,42 | (0,42 × 100)%, adică 42% |
După o clasificare corectă, suma frecvențelor absolute ale claselor va fi egală cu efectivul populației, iar suma frecvențelor relative ale claselor va fi 1, respectiv 100%.
Notă despre terminologie
În unele manuale din ASE, gruparea este denumită clasificare, iar reunirea câtorva grupe în condiții de universalitate și unicitate, pentru formarea de clase, nu este menționată. De exemplu, Mica Enciclopedie de Statistică (Trebici, 1985), o sursă de limbaj statistic din perioada când vorbirea bilingvă era inacceptabilă, declară clasa, grupa și modalitatea ca sinonime, cu înțelesul de “grupă” din acest document. Terminologia din acest capitol este cea din manualul Statistică și Econometrie, Tudorel Andrei (2003).
În alte manuale, prin clasificare se înțelege constituirea de submulțimi pe baza valorilor unei variabile calitative (de exemplu, cele trei submulțimi de județe descrise mai sus pe baza apartenenței regionale), iar gruparea este constituirea de submulțimi pe baza valorilor unei variabile cantitative, de regulă cu ajutorul unor intervale definitorii (de exemplu, localități cu altitudine 0-200 metri, localități cu altitudine 201-600 m, și localități cu altitudine peste 600 m, în demonstrația din Excel pentru noțiunile din acest capitol). Terminologia nu este strictă, diferind de la o disciplină științifică la alta, rămânând esențială ideea că o grupare/clasificare corectă este una în care nici un element nu este lăsat pe dinafară (universalitate / exhaustivitate) și niciunul nu este inclus în două submulțimi (unicitate / exclusivitate mutuală).
Tabel de contingență
Pentru exemplificare, voi folosi o bază de date populară, cea descriind pasagerii de pe ultima cursă a Titanicului (de exemplu, de la această adresă)
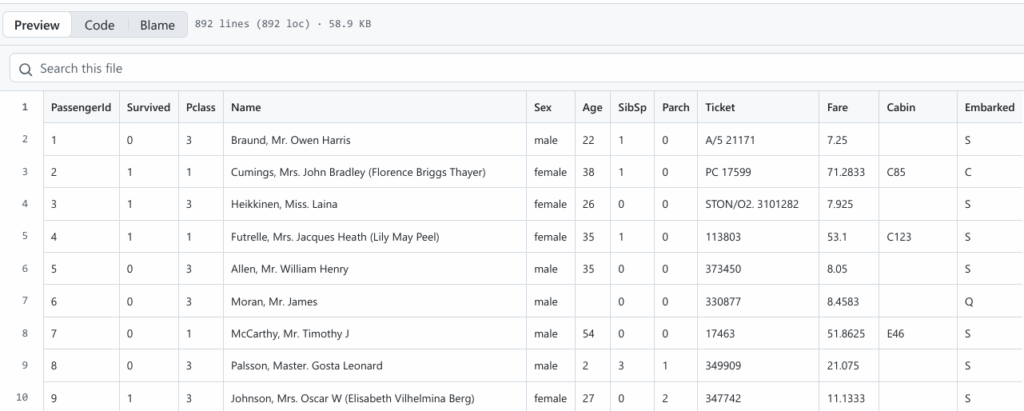
Această listă detaliază situația celor 891 pasageri, din care 342 au supraviețuit și 549 au decedat. Avem deci două submulțimi ale colectivității. Deoarece niciun pasager nu este lăsat în afara acestor două submulțimi, și niciunul nu este în ambele submulțimi, repartizarea pe aceste două submulțimi este o grupare. Funcția cu valorile n[“supraviețuitori”] = 342 și n[“decedați”] = 549 este o funcție de repartiție. Tabelul care ar descrie valorile sale este tabel de repartiție:
| Survived | Efectivul grupei (frecvență absolută) |
| 0 (No) | 342 |
| 1 (Yes) | 549 |
Seria de distribuție este ansamblul numerelor din a doua coloană, împreună cu identificatorii unităților statistice cărora le corespund. Seria este un concept, independent de forma în care o prezentăm.
- O descriere tipică a seriei este cea cu două șiruri în paranteze rotunde, șirul valorilor (342, 549), în combinație cu șirul descriptorilor (“supraviețuitori”, “decedați”).
- În alte cazuri, seria este descrisă cu perechi (valoare, identificator), ca, în ((342, “supraviețuitori”), (549, “decedați”)).
- Și tabelul de distribuție este o descriere, la fel de validă, a seriei de distribuție.
Se pot calcula și frecvențele relative, 342/891 ≈ 0,384 fiind proporția supraviețuitorilor, și 549 / 891 ≈ 0,616 fiind proporția decedaților.
Dintre cei 891 pasageri, 314 erau femei și 577 bărbați. Din nou inspectarea vizuală a datelor confirmă că, în seria de date din imagine, niciun pasager nu are sex neprecizat și niciun nu are mai mult de un sex, ceea ce înseamnă că și acestă repartizare pe submulțimi este o grupare. În lipsa informațiilor la nivel de unitate statistică, am putea verifica dacă suma frecvențelor absolute ale submulțimilor este egală cu efectivul colectivității (aici, 314 + 577 este egal cu 891), însă aceasta nu este o garanție, ci doar o indicație, că avem o grupare. (Aceeași egalitate este valabilă dacă am avea câteva persoane fără sex precizat și un număr egal de persoane cu două sexe.)
Tabelul de contingență (zis și tabel de asociere) sumarizează distribuția unei colectivități, când două metode distincte de grupare sunt posibile. Aici, putem descrie simultan repartiția pe cele două tipuri de grupare cu tabelul:
| Efective parțiale | Survived | |
| Sex | 0 (No) | 1 (Yes) |
| female | 81 | 233 |
| male | 468 | 109 |
Deci 81 de femei au decedat, 233 femei au supraviețuit. etc. Fiecare din numerele din tabel este un număr cardinal al unei submulțimi (“femei decedate” etc), deci sunt frecvențe absolute. În contextul tabelului de contingență, aceste frecvențe absolute descriind o submulțime indivizibilă se numesc efective parțiale. Pentru că am început cu grupări, nicio unitate statistică (persoană) nu poate aparține mai multor submulțimi și niciuna nu este lăsată în afara acestei repartiții, motiv pentru care suma efectivelor parțiale (81+233+468+109) va fi egală cu efectivul colectivității. Din nou, această verificare prin însumare este o indicație, nu o garanție, că avem un tabel de contingență.
De regulă, unui tabel de contingență i se adaugă totaluri la capetele fiecărei linii și coloane.
| Frecvențe absolute | Survived | ||
| Sex | 0 (No) | 1 (Yes) | Total |
| female | 81 | 233 | 314 |
| male | 468 | 109 | 577 |
| Total | 549 | 342 |
În contextul tabelului de contingență, astfel de frecvențe relative se numesc efective marginale. Se observă că totalurile pe linie, din ultima coloană, reconstituie frecvența absolută a grupelor de sex, așa cum sunt ele descrise în prima coloană. Dacă am păstra doar prima și ultima coloană, am reconstitui tabelul de distribuție pe sexe. Pentru că efectivele marginale însumând linii sunt o serie de distribuție, totalul lor (314+577) redă efectivul populației.
Similar, dacă am păstra doar prima și ultima linie, am reconstitui tabelul de distribuție pe deces/supraviețuire. Pentru că efectivele marginale însumând coloane sunt o serie de distribuție, totalul lor (549+342) redă efectivul populației. Prin urmare, tabelul de contingență se completează în colțul dreapta jos cu efectivul populației, care este simultan totalul efectivelor parțiale, totalul efectivelor marginale pe sexe, și totalul efectivelor marginale pe supraviețuire / deces.
| Frecvențe absolute | Survived | ||
| Sex | 0 (No) | 1 (Yes) | Total |
| female | 81 | 233 | 314 |
| male | 468 | 109 | 577 |
| Total | 549 | 342 | 891 |
Există trei tipuri de frecvență relativă în contextul unui tabel de contingență. Cel mai util este cel în raport cu totalul general, numit frecvență relativă parțială. De exemplu, 81 din cei 891 pasageri erau femei decedate, ceea ce corespunde unei proporții de 81/891 ≈ 0,091. Frecvența relativă parțială procentuală a femeilor decedate este deci cca 9,1% din totalul pasagerilor. Putem calcula și celelalte frecvențe relative parțiale:
| Frecvențe relative parțiale | Survived | |
| Sex | 0 (No) | 1 (Yes) |
| female | 81 / 891 ≈ 0,091 | 233 / 891 ≈ 0,262 |
| male | 468 / 891 ≈ 0,525 | 109 / 891 ≈ 0,122 |
Ca și în cazul efectivelor parțiale, putem adăuga sume la capătul fiecărei coloane și fiecărei linii:
| Frecvențe relative în raport cu efectivul colectivității | Survived | ||
| Sex | 0 (No) | 1 (Yes) | Total |
| female | 0,091 | 0,262 | 0,091 + 0,262 ≈ 0,352 |
| male | 0,525 | 0,122 | 0,525 + 0,122 ≈ 0,648 |
| Total | 0,091 + 0,525 ≈ 0,616 | 0,262 + 0,122 ≈ 0,384 |
În contextul tabelului de contingență, sumele de frecvențe relative parțiale se numesc frecvențe relative marginale. Dar, din nou, dacă am păstra numai prima și ultima linie, am reconstitui seria de distribuție pe deces/supraviețuire, cu frecvențe relative, descrisă în primul paragraf al acestei secțiuni. Similar, dacă am păstra numai prima și ultima coloană, am obține seria de distribuție pe sexe cu frecvențe relative: dintre pasageri, o proporție de 0,648 erau bărbați, iar o proporție de 0,352 erau femei. Cu alte cuvinte, frecvențele relative marginale se calculează fie ca sumă a liniei sau coloanei la care le-am atașat, fie ca raport între frecvența absolută a grupei (efectivul marginal pentru bărbați, femei, decedați etc.) și efectivul colectivității.
Un alt tip de frecvență relativă este cel condiționat, al cărei descriere completă include și numele grupării. Prin urmare, aici vom avea frecvență relativă condiționată de sex și frecvență relativă condiționată de supraviețuire/deces. Frecvența relativă condiționată de sex (uneori, frecvența relativă parțială condiționată) este cea în care aceleași efective parțiale din tabelul de contingență inițial vor fi descrise ca proporții din aceeași grupă de sex. De exemplu, cele 81 de femei decedate vor fi descrise ca proporție din totalul femeilor (314). Deci frecvența relativă condiționată de sex a femeilor decedate este 81 / 314 ≈ 0,258. Similar, restul frecvențelor relative condiționate de sex sunt:
| Frecvențe relative condiționate de sex | Survived | |
| Sex | 0 (No) | 1 (Yes) |
| female | 81 / 314 ≈ 0,258 | 233 / 314 ≈ 0,742 |
| male | 468 / 577 ≈ 0,811 | 109 / 577 ≈ 0,189 |
Tabelului de contingență cu frecvențe relative parțiale condiționate nu i se adaugă sume de linie sau coloană. Pe de o parte, în cazul frecvențelor condiționate de sex, fiecare serie de pe o linie este practic seria de distribuție în interiorul grupei descrise de acea linie. (De exemplu, în linia a doua, cele 314 femei au fost repartizate în 25,8% decedate și 74,2% supraviețuitoare.) Prin urmare, totalul pe fiecare linie va fi 100%. Pe de alta, totalul pe coloană nu are sens.
Similar, se pot calcula frecvențe relative parțiale condiționate de supraviețuire /deces:
| Frecvențe relative condiționate de supraviețuire / deces | Survived | |
| Sex | 0 (No) | 1 (Yes) |
| female | 81 / 549 ≈ 0,148 | 233 / 342 ≈ 0,681 |
| male | 468 / 549 ≈ 0,852 | 109 / 342 ≈ 0,319 |
În cazul frecvențelor relative condiționate de supraviețuire / deces, vom avea câte o serie de distribuție a grupei pe fiecare coloană, De exemplu, în coloana a doua, cei 549 decedați sunt, în proporție de 0,148 femei și în proporție de 0,852 bărbați. Deci totalul pe fiecare coloană va fi 1, iar totalul pe linie nu are sens.
Graficul cu coloane pentru grupări pe baza variabilelor nominale
Când înțelegerea unei serie de date univariate necesită comparații între valori, cel mai comun mod de a reprezenta grafic seria de date este utilizarea unor dreptunghiuri (zise coloane sau batoane; eng. bar) de lățime egală, egal spațiate, fiecare de înălțime proporțională cu valoarea variabilei.
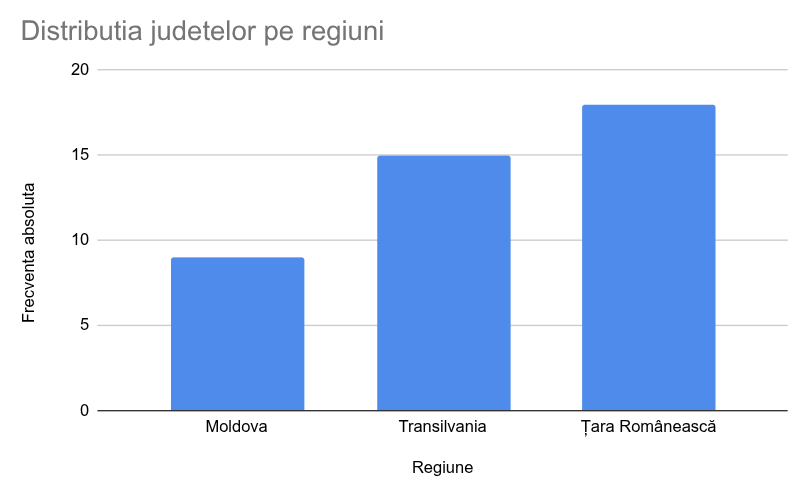
Când descriem o serie de distribuție putem folosi, la fel de bine, ca înălțime a coloanelor, fie frecvențele absolute, fie cele relative, ele fiind proporționale. De asemenea, putem folosi dreptunghiuri orizontale:
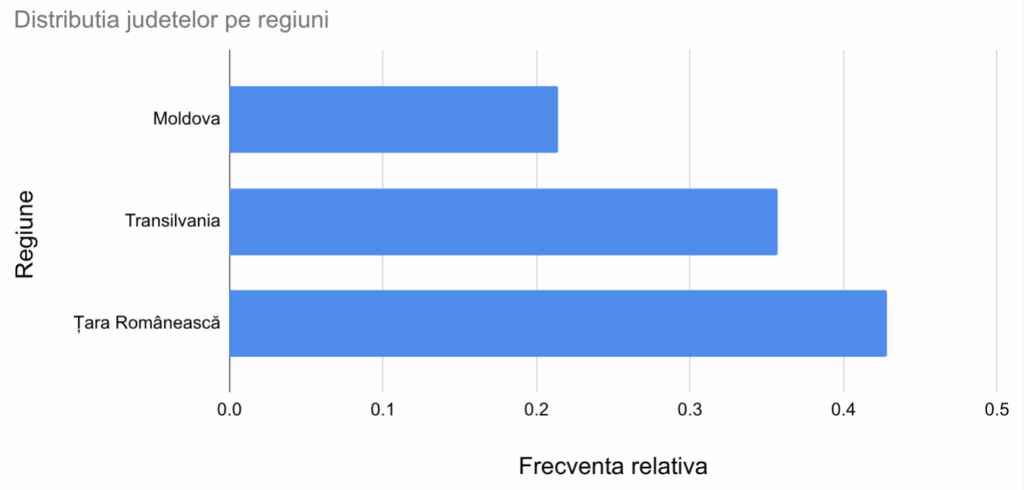
În cazul grupelor bazate pe o variabilă nominală, se poate opta pentru coloane separate (ca mai sus) sau bare adiacente:
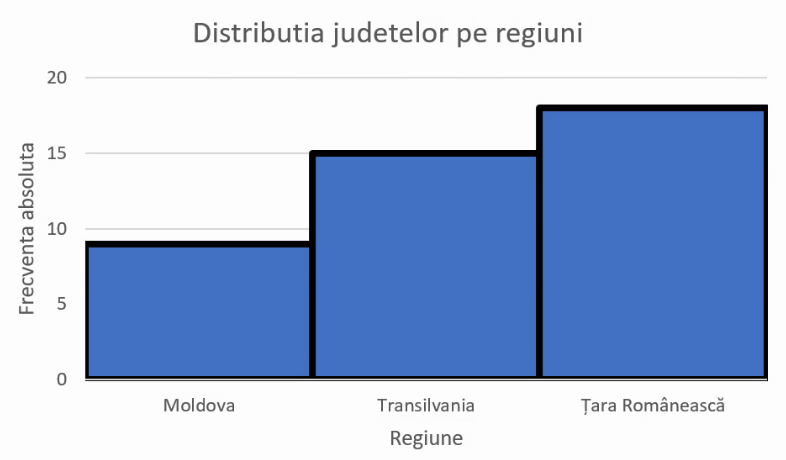
Pe axa ce descrie frecvențele, se folosesc aproape întotdeauna linii de rețea (eng. gridlines) în dreptul cărora se vor plasa etichete numerice (0, 5, 10 etc). Pe axa unde sunt descrie regiunile nu sunt folosite niciodată marcaje pe axă (eng. ticks) sau linii de rețea.
Barele adiacente pot fi greu de urmărit când numărul de grupe este mare. De asemenea, un grafic greu de urmărit este graficul cu sectoare, în care fiecărei grupe i se alocă un sector de arie proporțională cu frecvența:
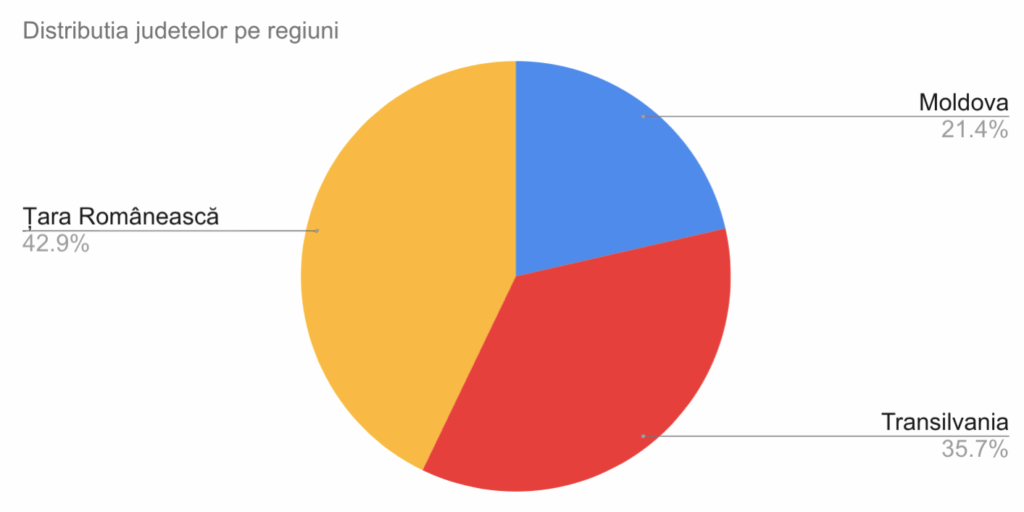
În ambele cazuri, coloană sau sector, dacă gruparea a fost făcută cu o variabilă calitativă, descrierea grupei va fi la mijlocul coloanei sau sectorului căreia îi corespunde. La grupări cu variabile cantitative, este preferabil ca descrierile de pe axa grupelor să fie între coloane (vezi mai jos).
Alte forme de prezentare pentru comparații, similare cu cele pe sectoare ca principiu (proporționalitatea valorii cu aria), sunt cele cu pătrate sau cercuri. Dacă am reprezenta ca bare populația omenirii pe țări, vom avea dificultăți prin prisma faptului că China are o populație de cca 36 de mii de ori mai mare decât Monaco. Fie coloana pentru Monaco va fi extrem de mică, fie coloana pentru China nu va intra în imagine, și deci nu vom putea face comparații vizuale. Prin folosirea de pătrate sau cercuri, va fi suficient să folosim un cerc cât ecranul / foaia pentru China, și unul de cca 190 de ori mai scund pentru Monaco:
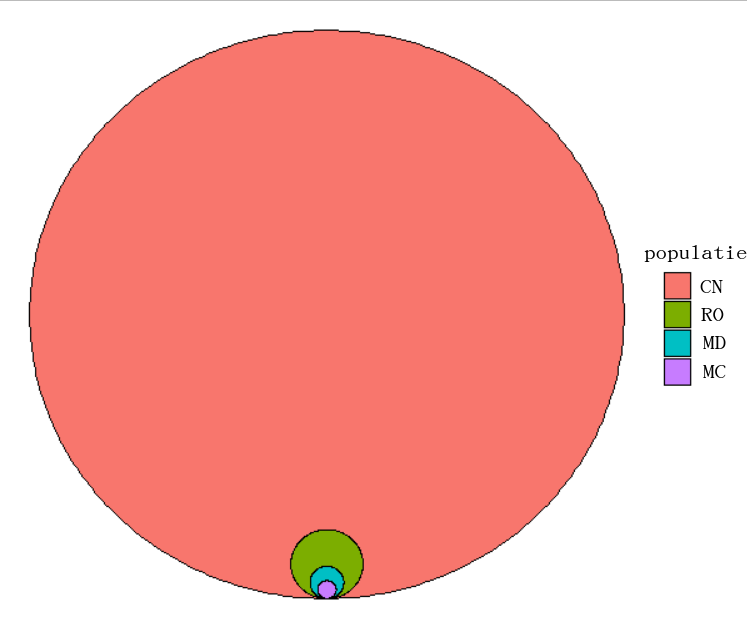
Un cerc cu diametrul de 190 de ori mai mare decât altul are o suprafață de 190² = 36100 ori mai mare. Același avantaj există la reprezentarea cu pătrate, aria pătratului crescând proporțional cu pătratul (sic) laturii:
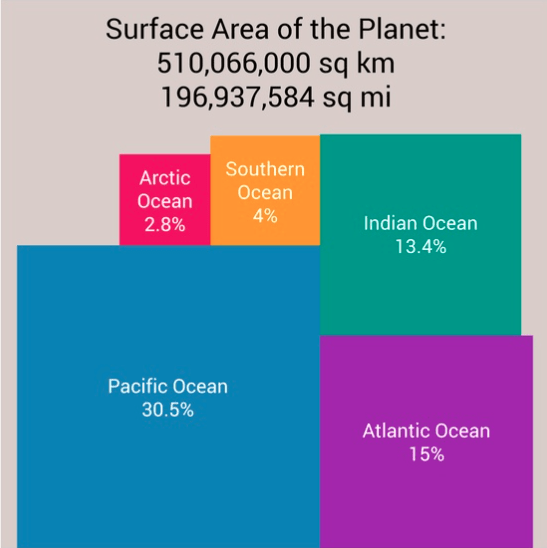
Revenind la primul exemplu, coincidența face ca seria de distribuție a județelor să aibă caracter spațial. Se poate reprezenta această informație și sub forma unei hărți, care va arăta interesant, dar va anula orice șansă de a compara cele trei frecvențe:
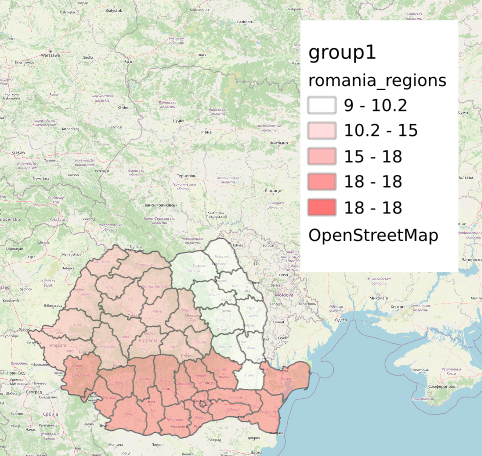
Coloanele cu baza la același nivel, pornind de la zero, sunt cel mai bun mod de a reprezenta comparativ un grup de numere, așa cum este seria de distribuție. Presa destinată publicului larg practică modificarea axei cantitative, mutând originea coloanelor aproape de vârful lor, pentru a amplifica, de regulă nejustificat, mărimea diferențelor. De exemplu, prin mutarea bazei coloanelor la 8, putem arăta o Moldovă aparent mult mai mică:
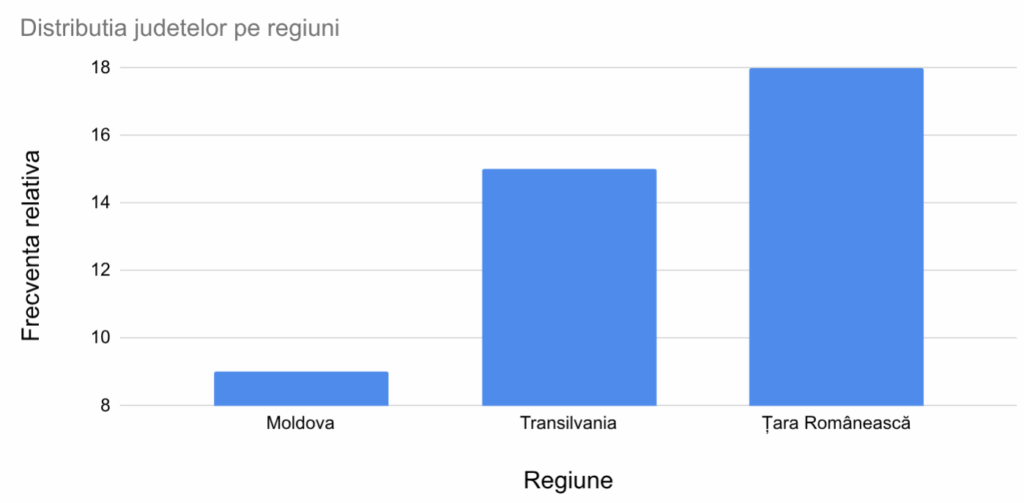
Grafice cu coloane pentru tabel de contingență
Dacă numărul submulțimilor descrise de un tabel de contingență este mic, se poate folosi un aranjament similar, cu coloane proporționale ca lungime cu frecvența absolută a submulțimii. În exemplul pasagerilor de pe Titanic, cu doar 4 submulțimi:
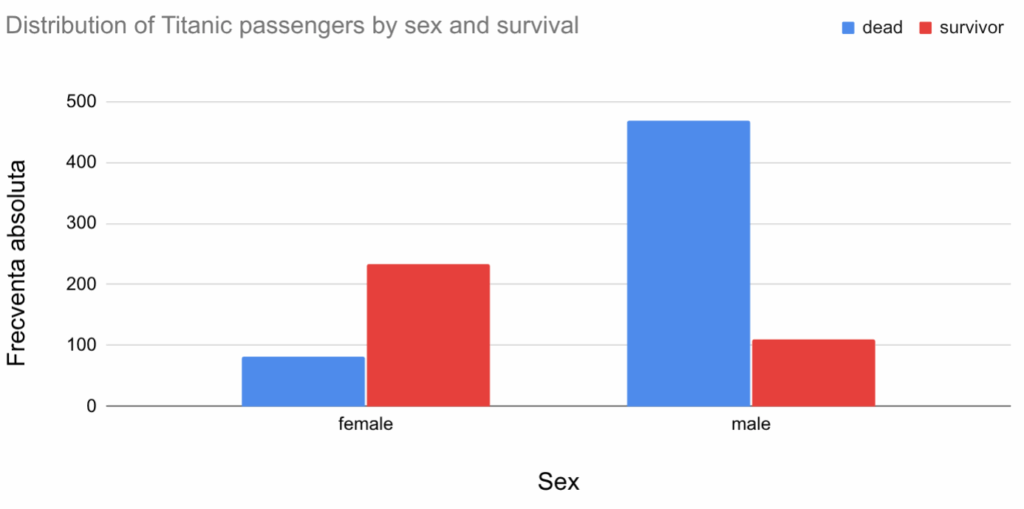
Se pot folosi distanțe mai mari între grupuri (aici, sexul) și culori diferite pentru identificare celuilalt tip de grupare (aici, supraviețuirea). Pentru diferențe de culoare va fi necesară o legendă.
În cazul coloanelor distincte pentru fiecare submulțime, se pot face comparații pentru fiecare pereche de submulțime, chiar și cele absurde (erau mai mulți bărbați decedați decât femei supraviețuitoare?). Mai frecvent se rearanjează coloanele, prin etajare (eng. stacking), pentru ca fiecare coloană să descrie o serie de distribuție pe frecvențe absolute din interiorul unei grupe:
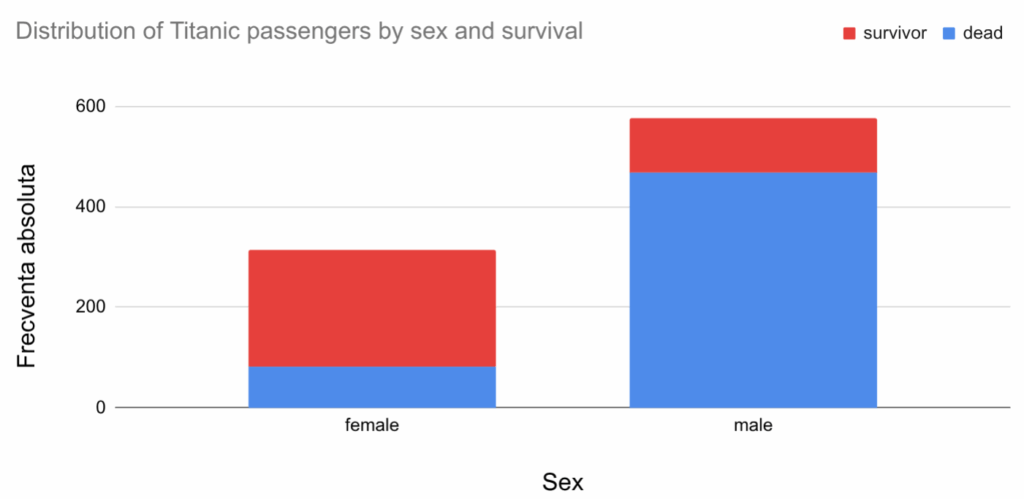
Astfel, putem compara direct numai seria de distribuție pe sexe și cel mult cele două submulțimi de la baza graficului (femei decedate vs bărbați decedați), și se transmite numai o idee generală despre distribuția în interiorul fiecărei grupe (la femei sunt mai multe supraviețuiri, la bărbați, mai multe decese). Totuși, când există multe grupe, graficul fără etajare devine prea încărcat, motiv pentru care se va prefera grafic etajat.
O alternativă la coloanele etajate o reprezintă graficul treemap, în care fiecare submulțime este reprezentată cu un dreptunghi de suprafață proporțională cu numerele pe care dorim să le reprezentăm, iar o grupare este indicată cu culori:
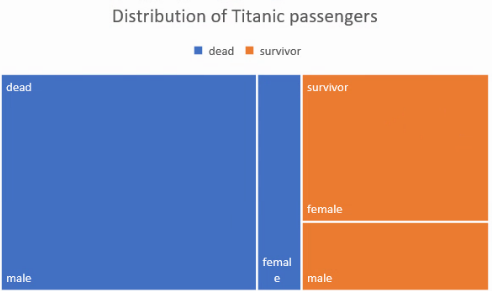
Această reprezentare este preferată când subdiviziunile fiecărei grupe de culoare diferă, când numărul de subdiviziuni al unei grupe este mari și / sau când numerele se întind pe un interval amplu:
Grupare după valorile unei variabile cantitative
Variabilele calitative sunt în principiu discontinue, ceea ce limitează numărul de grupări posibile la un număr finit de combinații. Cu trei valori posibile, nu pot avea decât
- o grupare care să creeze trei submulțimi
- trei grupări în care una din variante definește o grup iar celelalte două – cealaltă grupă
- o grupare cu o singură submulțime pentru toate valorile posibile.
Variabilele cantitative sunt cel mai adesea discontinue, ceea ce implică un număr infinit de grupări posibile. Pentru trei valori numerice, putem împărți universul valorilor posibile în
- intervale din 10 în 10 (grupa unităților statistice cu valori de la 0 la 9,999; grupa 10-19,999; etc)
- intervale din 100 în 100 (grupa 0-99,99; grupa 100-199,99; etc)
- intervale din 1000 în 1000 etc.
Orice număr este posibil. Mai mult, intervalele pot fi de dimensiuni diferite (0-9,999; 10-29,999; 30-49,999 etc.) Deși majoritatea acestor grupări sunt inutile, un număr relativ mare de opțiuni acceptabile este posibil.
Spunem că variabilele calitative permit construirea de serii de distribuție simple, atunci când fiecare grupă este definită de o singură valoare a respectivei variabilei. Prin contrast, dacă grupăm pe baza unei variabile cantitative, pe care o comparăm cu o serie de intervale, vom obține o serie de distribuție grupată.
Didactic, cea mai simplă serie de distribuție grupată se numește stem and leaf, și grupează împreună numere cu același prefix (stem). De exemplu, date fiind numerele (10, 11, 17, 21, 25, 35, 54), vom construi următoarele grupe:
- stem 1: 10, 11, 17
- stem 2: 21, 25
- stem 3: 35
- stem 4: –
- stem 5: 54.
Acestă grupare se descrie cu un tabel de distribuție de forma:
| Stem | Componente |
| 1 | 10, 11, 17 |
| 2 | 21, 25 |
| 3 | 35 |
| 4 | – |
| 5 | 54 |
Practic, am grupat numerele după apartenența la următoarele intervale
| Interval | Componente |
| 10-19 | 10, 11, 17 |
| 20-29 | 21, 25 |
| 30-39 | 35 |
| 40-49 | – |
| 50-59 | 54 |
Acest exemplu este elocvent pentru modul cum se definesc intervalele în statistica descriptivă. Ca și intervalele din matematică, intervalele de grupare din statistică sunt adiacente una la alta, însă scrierea matematică cu interval semideschis, [10, 20), nu este indicat, mai ales în comunicarea cu publicul larg. Vom formula descrierile de așa natură încât să fie clar cărui interval, dintre cele două adiacente, îi aparține valoarea separatoare, chiar și unui cititor care nu cunoaște sensul cuvintelor “interval închis” și “interval deschis”.
- Aici, vom scrie în loc de [10, 20), un text de forma “între 10 și 19”.
- Dacă lucram cu intervale deschise inferior, am fi înlocuit (30, 40], ]n comunicarea cu publicul larg, cu “între 31 și 40”.
Pentru următoarele noțiuni, am revenit la seria de date despre ultimii pasageri ai Titanicului:
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked |
| 1 | 0 | 3 | Braund | male | 22 | 1 | 0 | A/5 21171 | 7.25 | S | |
| 2 | 1 | 1 | Cumings | female | 38 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen | female | 26 | 0 | 0 | STON/O2. 3101282 | 7.925 | S | |
| 4 | 1 | 1 | Futrelle | female | 35 | 1 | 0 | 113803 | 53.1 | C123 | S |
| 5 | 0 | 3 | Allen | male | 35 | 0 | 0 | 373450 | 8.05 | S | |
| 6 | … |
Prin discretizare, putem crea o variabilă care să descrie, pentru fiecare din aceștia, în ce decadă a vieții se află:
| PassengerId | … | Age | … | Age bin |
| 1 | … | 22 | … | 20 – 29 |
| 2 | … | 38 | … | 30 – 39 |
| 3 | … | 26 | … | 20 – 29 |
| 4 | … | 35 | … | 30 – 39 |
| 5 | … | 35 | … | 30 – 39 |
| 6 | … | … | missing | |
| 7 | … | 54 | … | 50 – 59 |
| 8 | … | 2 | … | 0 – 9 |
| 9 | … | 27 | … | 20 – 29 |
| 10 | … | 14 | … | 10 – 19 |
| 11 | … | 4 | … | 0 – 9 |
Acest table se poate rearanja, în pregătirea seriei de distribuție grupată, ca stem and leaf, astfel:
| Interval de vârstă (ani) | Passenger IDs |
| 0-9,9 | 8, 11, 17, … |
| 10-19,9 | 10, 15, 23, … |
| 20-29,9 | 1, 3, 9, … |
| 30-39,9 | 2, 4, 5, … |
| 40-49,9 | 31, 36, 41, … |
| 50-59,9 | 7, 12, 16, … |
| 60-69,9 | 34, 55, 171, … |
| 70-79,9 | 97, 117, 494, … |
| 80-89,9 | 631 |
| missing | 6, 18, 20, … |
(A fost necesară scrierea cu zecimală, 9,9, în loc de 9, deoarece în tabel există și vârste fracționale.)
Enumerarea unităților statistice permită numărarea lor:
| Interval de vârstă (ani) | Frecvențe absolute |
| 0-9,9 | 62 |
| 10-19,9 | 102 |
| 20-29,9 | 220 |
| 30-39,9 | 167 |
| 40-49,9 | 89 |
| 50-59,9 | 48 |
| 60-69,9 | 19 |
| 70-79,9 | 6 |
| 80-89,9 | 1 |
| missing | 177 |
Ultimul tabel este un tabel de distribuție, descriind frecvențele absolute pentru fiecare interval de vârstă. Din cei 891 pasageri cunoscuți, 177 nu au vârsta precizată, așa că va trebui să definim o nouă colectivitate, “pasagerii Titanicului cu vârstă cunoscută”. Seria de distribuție a acestei noi colectivități pe intervale de vârstă va fi descrisă de un tabel ca cel precedent, cu omisiunea ultimei linii:
| Interval de vârstă (ani) | Frecvențe absolute |
| 0-9,9 | 62 |
| 10-19,9 | 102 |
| 20-29,9 | 220 |
| 30-39,9 | 167 |
| 40-49,9 | 89 |
| 50-59,9 | 48 |
| 60-69,9 | 19 |
| 70-79,9 | 6 |
| 80-89,9 | 1 |
Spre deosebire de penultimul tabel, cel din urmă descrie o serie de distribuție grupată, cu frecvențe absolute, toate submulțimile sale fiind definite de intervale numerice.
Efectivul noii colectivități este suma 62+ 102 + … + 6 + 1 = 714. Cu ajutorul acestui total, putem calcula componentele seriei de distribuție grupată cu frecvențe relative:
| Interval de vârstă (ani) | Frecvențe relative |
| 0-9,9 | 62 / 714 ≈ 0.087 |
| 10-19,9 | 102 / 714 ≈ 0.143 |
| 20-29,9 | 220 / 714 ≈ 0.308 |
| 30-39,9 | 167 / 714 ≈ 0.234 |
| 40-49,9 | 89 / 714 ≈ 0.125 |
| 50-59,9 | 48 / 714 ≈ 0.067 |
| 60-69,9 | 19 / 714 ≈ 0.027 |
| 70-79,9 | 6 / 714 ≈ 0.008 |
| 80-89,9 | 1 / 714 ≈ 0.001 |
Dacă seria de distribuție pe frecvențe absolute indica un număr mare de tineri (220 cu vârste între 20 și 29,9 ani; 102 cu vârste între 10 și 19,9 ani), seria de distribuție pe frecvențe relative indică și mai clar preponderența tinerilor pe o navă care pleca din Marea Britanie către SUA. Frecvența relativă a grupei de vârstă 20-29,9 ani este 0,308, adică cca 31% dintre pasageri aveau între 20 și 29,9 ani.
Histograma
Reprezentarea grafică a seriei de distribuție grupate se face tot cu coloane, în primă instanță, ca și la seria de distribuție simplă. Deosebirea esențială este că, în cazul distribuțiilor pe interval, se preferă marcajele (eng. ticks) și etichetele (eng. labels) între coloane, nu la mijlocul coloanei, pe axa grupelor:
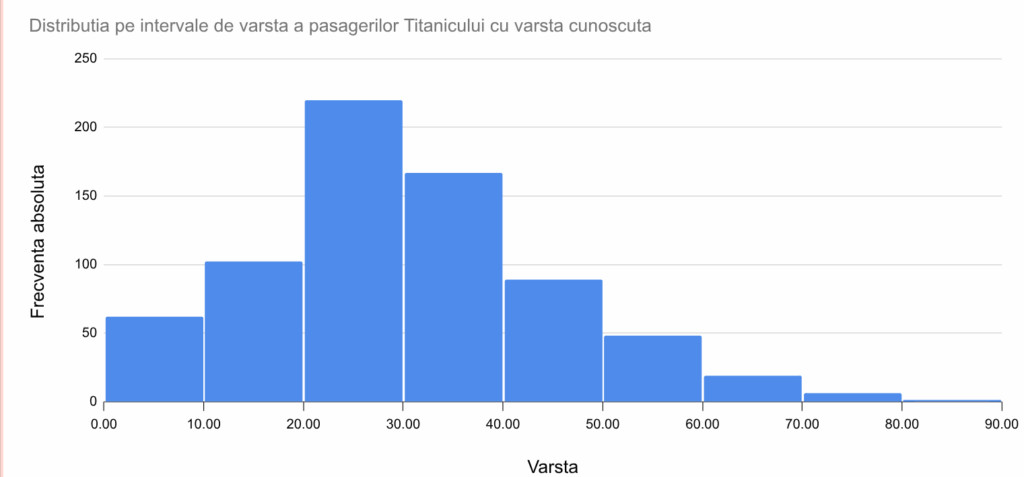
Seriile de distribuție bazate pe variabile nominale sunt cele la care toate diferențele sunt egal tratate. O consecință este că reprezentarea grafică a acestor serii de distribuție nu va fixa poziția coloanelor pe axa grupelor. În afară de convenția că lățimea coloanelor să fie egală, pentru ca și înălțimile, și ariile să fie proporționale cu datele prezentate, nu am fixat în niciun fel pozițiile. În secțiunea de mai sus, la reprezentarea grafică a tabelului de contingență, ați văzut grafice cu coloane cu spațiere variabilă. Seriile de distribuție la care diferențele sunt tratate identic, cum sunt cele dezvoltate pe baza unei variabile nominale, se numesc serii de distribuție homograde, iar reprezentarea lor grafică nu necesită controlul strict al poziției coloanei pe axa grupelor, .
Prin contrast, la seriile de distribuție pe intervale, se poate măsura diferența dintre grupe. Diferența dintre grupele “0-9,9 ani” și “10-19,9 ani” este de cinci ori mai relevantă decât distanța dintre “0-9,9 ani” și “50-59,9 ani”, motiv pentru care și distanța dintre coloane va fi, în al doilea caz, de precis 5 ori mai mare. Astfel, poziția pe axa pe care descriem grupele nu mai este arbitrară. Este necesar ca limitele dintre coloane să fie plasate în poziția indicată de număr. În exemplul de mai sus, trebuie ca marcajele de la 0, 10, 20, 30 etc să se afle în pozițiile care ar corespunde punctelor de coordonate (0,0), (10,0), (20,0), (30,0) etc. O serie de distribuție la care se poate calcula un grad mai mare sau mai mic de apropiere se numește serie de date heterogradă, iar reprezentarea lor grafică va necesita coloane de poziție și lățime precise.
Reprezentarea grafică cu coloane a unei serii de distribuție heterogradă se mai numește histogramă. De regulă, intervalele definitorii pentru grupele pe care s-a construit histograma sunt adiacente, situație în care și coloanele din histogramă vor fi adiacente.
Histograme cu coloane de lățime variabilă
Nu este strict necesar ca lățimile coloanelor din histogramă să fie egale. Este necesar numai ca aria coloanelor să fie proporțională cu frecvența reprezentată. De exemplu, tabelul de distribuție poate fi unul cu intervale inegale:
| Vârste | Frecvență absolută |
| 0-20 | 20 |
| 20-30 | 10 |
| 30-40 | 20 |
| 40-50 | 40 |
În acest caz, vom avea coloane de la x=0 la x=20, de la x=20 la x=30, de la x=30 la x=40 etc., cu prima coloană de două ori mai lată decât celelalte. Pentru a face aria proporțională cu fiecare din frecvențele absolute, va fi necesar să facem coloana intervalului 0-20 de două ori mai scundă decât ar fi fost indicat de o frecvență de 20. Astfel, coloana intervalului 0-20 va avea aceeași înălțime cu coloana intervalului 20-30:
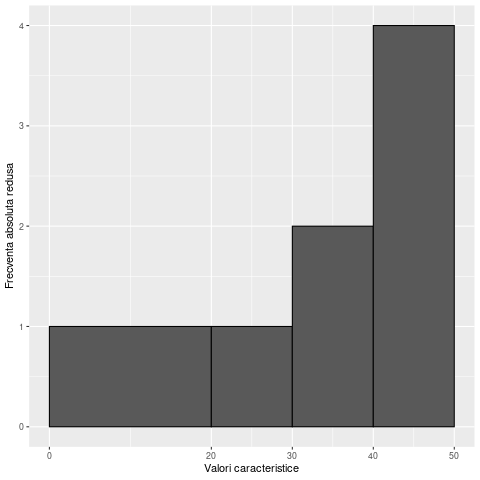
Fiindcă aceeași poziție pe axa coordonatelor, codifică pentru intervalul 0-20 o frecvență absolută de 20, iar pentru intervalul 20-30 o frecvență absolută de 10, axa coordonatelor nu va mai putea fi etichetată “frecvențe absolute”.
Poligonul frecvențelor
În exemplul Titanicului, am identificat 6 pasageri cu vărste între 70 și 79,9 ani. Pe histogramă, intervalul “70-79,9 ani” (in realitate interval închis inferior și deschis superior, aici [70, 80)) este reprezentat de o bară ce se întinde de la x=70 la x=80. Latura sa superioară se află la frecvența absolută, y = 6. În această secțiune, și în multe alte cazuri, poate fi necesar să aproximăm valoarea unei variabile ca număr unic, deși tot ce ni se va oferi este o serie de distribuție pe intervale (perechi de numere). În astfel de situații, cel mai comun mod de aproximare este cel ce folosește mijlocul intervalului, adică media aritmetică a celor două limite de interval. Aici, în lipsa altor informații, vom spune că cei 6 pasageri au vârsta de cca 75 ani.
În lipsa seriei de date, putem aproxima vârsta tuturor membrilor de grupă de interval cu mijlocul intervalului
| Interval de vârstă (ani) | Cea mai probabilă vârstă | Frecvențe absolute |
| 0-9,9 | 5 | 62 |
| 10-19,9 | 15 | 102 |
| 20-29,9 | 25 | 220 |
| 30-39,9 | 35 | 167 |
| 40-49,9 | 45 | 89 |
| 50-59,9 | 55 | 48 |
| 60-69,9 | 65 | 19 |
| 70-79,9 | 75 | 6 |
| 80-89,9 | 85 | 1 |
Putem reprezenta grafic aceste vărste probabile pentru fiecare interval, împreună cu numărul lor (frecvența absolută):
| Interval de vârstă (ani) | Coordonată X (mijlocul intervalului) | Coordonată Y (poziția marginii superioare a coloanei) |
| 0-9,9 | 5 | 62 |
| 10-19,9 | 15 | 102 |
| 20-29,9 | 25 | 220 |
| 30-39,9 | 35 | 167 |
| 40-49,9 | 45 | 89 |
| 50-59,9 | 55 | 48 |
| 60-69,9 | 65 | 19 |
| 70-79,9 | 75 | 6 |
| 80-89,9 | 85 | 1 |
O imagine mai clară a ce va reprezenta acest grafic o obținem dacă vom pune punctele pe același grafic cu histograma:
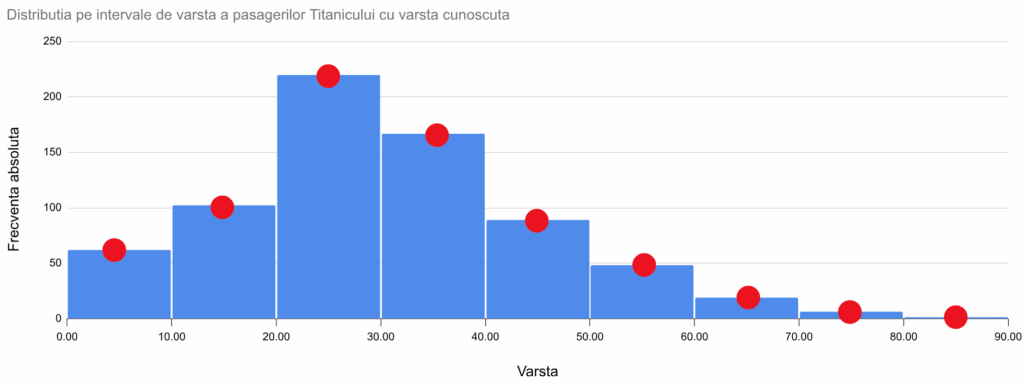
Fiecare punct de mai sus este pe mijlocul laturii superioare a coloanei cu care e reprezentat intervalul. O linie care unește mijloacele laturilor superioare ale coloanelor din histogramă, cu adaosurile descrise mai jos, se numește poligon al frecvențelor:
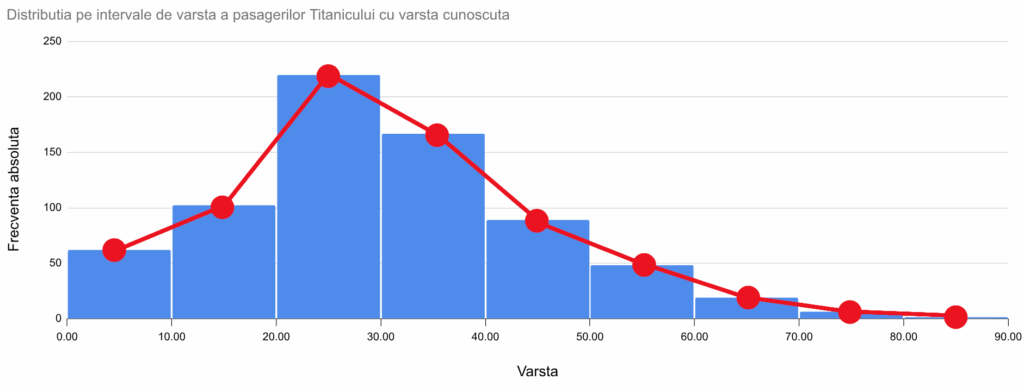
Pentru ca un poligon al frecvențelor să fie complet, este necesar ca, la fiecare capăt al distribuției să fie adus la axa absciselor. În acest exemplu, chiar și în lipsa informațiilor despre indivizi, știm din seria de distribuție că nu există pasageri mai tineri de zero ani sau mai bătrâni de 90 de ani. Cu alte cuvinte, frecvențele relative la 0 și 90 ani vor fi nule. Vom aduce poligonul frecvențelor axa grupelor (aici, la y=0), prin suplimentarea tabelului de mai sus cu două puncte la (0,0) și la (90,0).
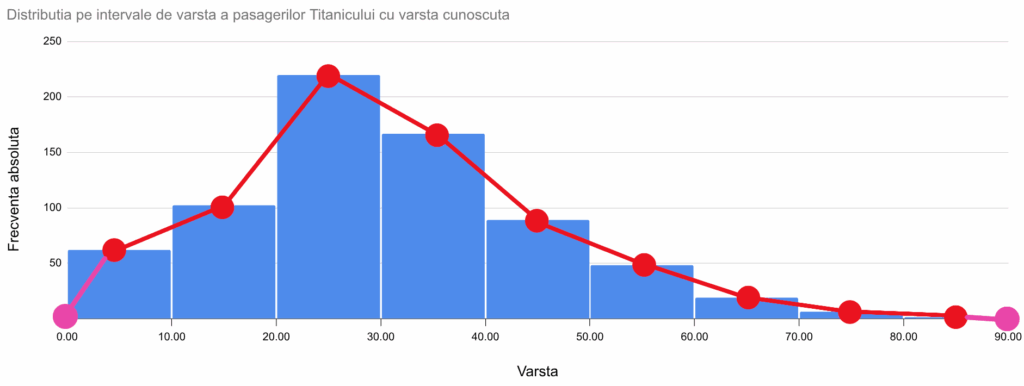
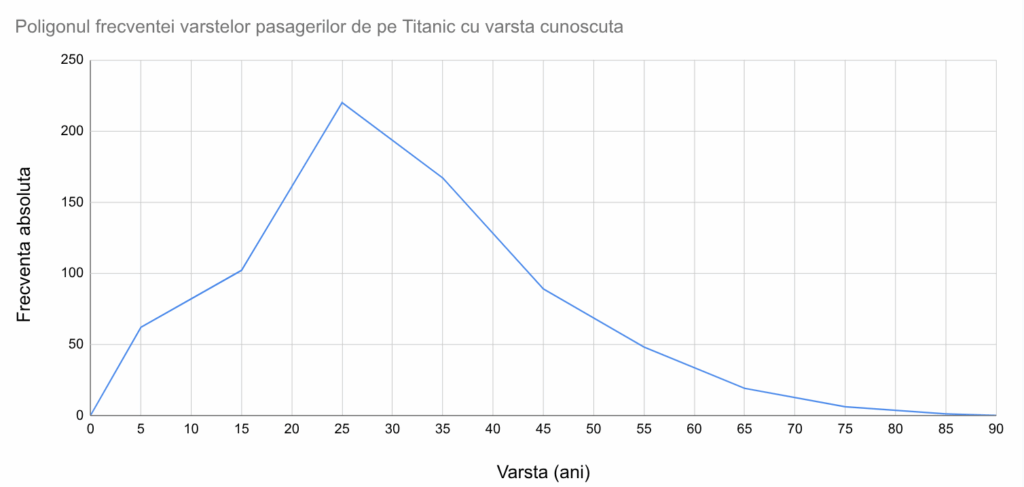
Păstrând doar poligonul frecvențelor, vom reprezenta seria de distribuție a vârstelor pasagerilor de pe Titanic astfel:
Frecvențe cumulative
Pe lângă grupele definite de intervale de valori (cele cu roșu/roz în imaginea de mai jos; de exemplu “pasageri între 10 și 19,9 ani”, adică [10,20)), putem construi și perechi de clase în baza fiecărei limite. În primul rând, fiecare limită poate fi marginea superioară a unui interval de valorilor posibile (verde); de exemplu pasageri cu mai puțin de 20 de ani, adică (-∞, 20). Pentru n limite, vom avea n asemenea intervale.
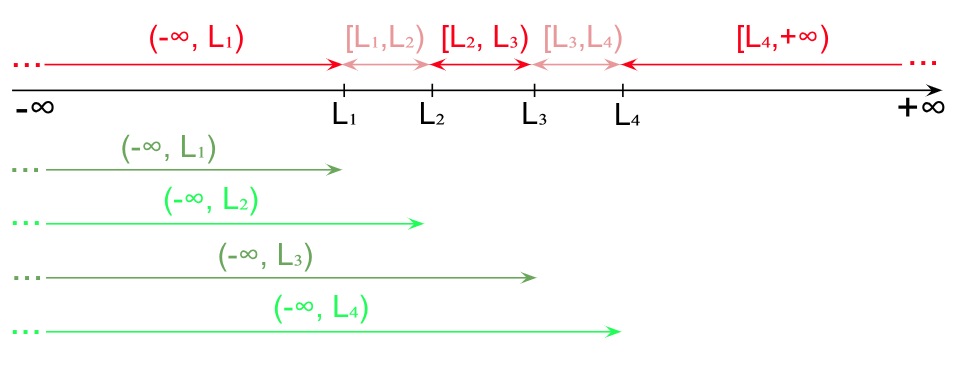
Pentru fiecare dintre aceste intervale de valori, putem selecta o submulțime a colectivității. Pentru exemplificare, vom completa seria de distribuție a vârstelor pasagerilor de pe Titanic cu cele două grupe de interval semimărginit:
| Interval de vârstă (ani) | Frecvențe absolute |
| sub 0 | 0 |
| 0-9,9 | 62 |
| 10-19,9 | 102 |
| 20-29,9 | 220 |
| 30-39,9 | 167 |
| 40-49,9 | 89 |
| 50-59,9 | 48 |
| 60-69,9 | 19 |
| 70-79,9 | 6 |
| 80-89,9 | 1 |
| cel puțin 90 | 0 |
De exemplu, clasa pasagerilor de pe Titanic cu vârste cunoscute de mai puțin 40 de ani ar fi reuniunea grupelor
- persoane cu vârsta între 30 și 39,9 ani
- persoane cu vârsta între 20 și 29,9 ani
- persoane cu vârsta între 10 și 19,9 ani
- persoane cu vârsta între 0 și 9,9 ani
- persoane cu vârsta sub 0 (între -∞ și zeroș absurdă, dar inclusă pentru exemplificarea principiului general).
Cum niciun pasager nu poate fi în mai mult de una din aceste cinci grupe, nu este necesar să cunoaștem seria de date pentru a descrie câte unități statistice sunt în acea submulțime, fiind suficiente informațiile din seria de distribuție. Frecvența absolută a pasagerilor de pe Titanic cu vârste cunoscute de mai puțin 40 de ani este suma frecvențelor absolute ale grupelor de mai sus:
- 167 persoane cu vârsta între 30 și 39,9 ani
- 220 persoane cu vârsta între 20 și 29,9 ani
- 102 persoane cu vârsta între 10 și 19,9 ani
- 62 persoane cu vârsta între 0 și 9,9 ani
- 0 persoane cu vârsta sub 0.
Frecvența absolută a pasagerilor de pe Titanic cu vârste cunoscute de mai puțin 40 de ani este deci 0+62+102+220+167 = 551.
Similar, pentru orice limită X, putem defini fiecare submulțime “mai tânăr de X ani”, și putem calcula frecvența absolută în fiecare dintre aceste submulțimi, exclusiv pe baza seriei de distribuție:
| Interval de vârstă (ani) | Grupe componente | Frecvențe absolute cumulative ascendente |
| sub 10 ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani” | 0 + 62 = 62 |
| sub 20 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani” și “10-19,9 ani” | 0 + 62 + 102 = 164 |
| sub 30 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani” și “20-29,9 ani” | 0 + 62 + 102 + 220 = 384 |
| sub 40 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani” și “30-39,9 ani” | 0 + 62 + 102 + 220 + 167 = 551 |
| sub 50 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani” și “40-49,9 ani” | 0 + 62 + 102 + 220 + 167 + 89 = 640 |
| sub 60 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani” și “50-59,9 ani” | 0 + 62 + 102 + 220 + 167 + 89 + 48 = 688 |
| sub 70 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani” “50-59,9 ani”, și “60-69,9 ani” | 0 + 62 + 102 + 220 + 167 + 89 + 48 + 19 = 707 |
| sub 80 de ani | “persoane cu vârsta între -∞ și zero”, 0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani” “50-59,9 ani”, “60-69,9 ani” și “70-79,9 ani” | 0 + 62 + 102 + 220 + 167 + 89 + 48 + 19 + 6 = 713 |
| sub 90 de ani | “persoane cu vârsta între -∞ și zero”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani” “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani” și “80-89,9 ani” | 0 + 62 + 102 + 220 + 167 + 89 + 48 + 19 + 6 + 1 = 714 |
Șirul acestor frecvențe absolute pentru intervale de la -∞ până la fiecare din limitele de interval cu care s-au definit deja grupe pe interval se numește serie de frecvențe cumulative ascendente.
Variații:
- În funcție de informațiile pe care le aveți despre variabila de grupare, puteți înlocui -∞ cu o valoare finită, cu condiția să fie mai mică sau egală cu cea mai mică valoare posibilă. De exemplu, este la fel de acceptabil să folosiți -0 în loc de -∞ pentru vârstele umane, clasa “mai puțin de 20 de ani” fiind la fel de bine definită ca:
- submulțimea pasagerilor cu vârstă în intervalul (-∞, 20)
- submulțimea pasagerilor cu vârstă în intervalul [0, 20).
- Modul în care sunt folosite limitele în seria de distribuție va schimba descrierea verbală și simbolică a claselor.
- În exemplul Titanicului, am definit intervale de vărstă deschise la limita superioară ([10,20), [20,30), [30,40), etc), așa că și seria de frecvențe cumulative ascendente va avea clase deschise superior ((-∞, 20), (-∞, 30), (-∞, 40) etc). Pe baza seriei de distribuție din secțiunea precedentă nu putem ști câte persoane au precis 40 de ani, și deci nu putem calcula o frecvență a pasagerilor cu cel mult 40 ani adică a celor cu vârstă în intervalul închis (-∞, 40]. Putem calcula doar o frecvență a pasagerilor cu mai puțin de 40 ani adică a celor cu vârstă în intervalul deschis (-∞, 40).
- În cazurile când seria de distribuție se bazează pe intervale închise superior (aici ar fi fost (10, 20], {20, 30], (30, 40], care ar fi fost descrise “între 10,1 și 20 ani”, “între 20,1 și 30 ani”, “între 30,1 și 40 ani”), intervalele pentru frecvențe cumulative ar fi și ele închise superior ((-∞, 20], (-∞, 30], (-∞, 40], descrise ca vârste “mai puțin sau egale cu 20 ani”, “mai puțin sau egale cu 30 ani”, “mai puțin sau egale cu 40 ani” etc).
Convențional, la finalul acestei serii de intervale, se mai adaugă o mulțime și mai vastă, cea care comasează toate grupele de interval (de regulă, corespunzând mulțimii numerelor reale; verde deschis mai jos). Efectivul său va fi efectivul colectivității.
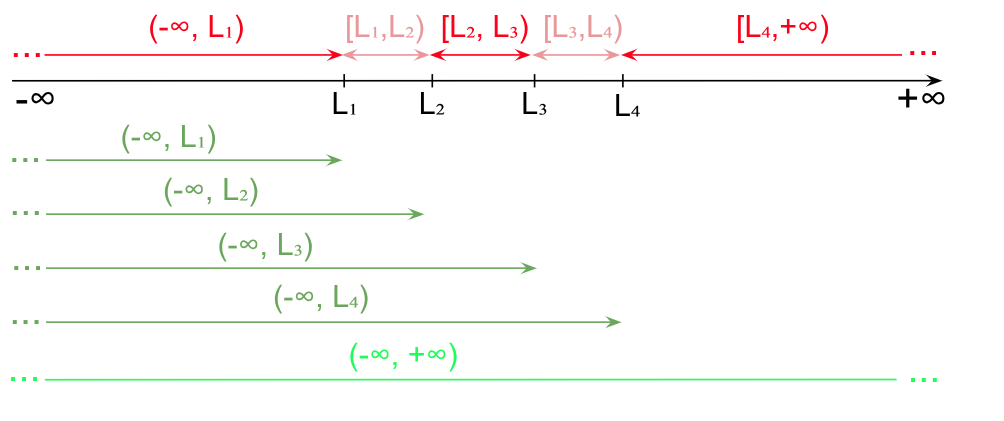
Toate clasele de mai sus nu sunt doar o reuniune de grupe, dar pot fi concepute și ca o reuniune a clasei precedente cu o singură grupă. De exemplu, clasa pasagerilor cu “mai puțin de 20 de ani” este și reuniunea
- clasei pasagerilor în vârstă “mai puțin de 10 de ani” cu
- grupa pasagerilor de “10-19.9 ani”.
Cele două componente ale reuniunii sunt disjuncte, și deci frecvența absolută a clasei “mai puțin de 20 de ani” va fi suma
- clasei pasagerilor în vârstă “mai puțin de 10 de ani” (62) cu
- grupa pasagerilor de “10-19.9 ani” (102).
La modul general, valorile caracteristice cuprinse în intervalul portocaliu trebuie să fie în unul și numai unul din intervalele violete:
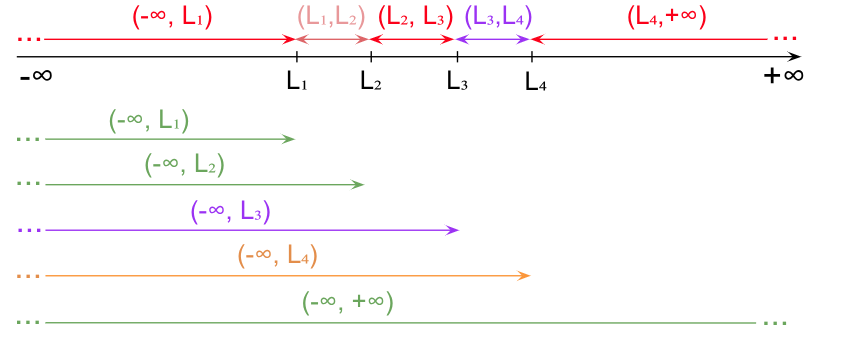
Deci frecvențele absolute cumulative crescătoare pot fi calculate din frecvența absolută cumulativă precedentă, prin adunarea frecvenței încă unei grupe:
| Interval de vârstă (ani) | Construcție echivalentă | Frecvențe absolute cumulative ascendente |
| sub 10 de ani | “sub 0 ani” și “0-9,9 ani” | 0+62 = 62 |
| sub 20 de ani | “sub 10 ani” și “10-19,9 ani” | 62 + 102 = 164 |
| sub 30 de ani | “sub 20 ani” și “20-29,9 ani” | 164 + 220 = 384 |
| sub 40 de ani | “sub 30 ani” și “30-39,9 ani” | 384+167 = 551 |
| sub 50 de ani | “sub 40 ani” și “40-49,9 ani” | 551+89 = 640 |
| sub 60 de ani | “sub 50 ani” și “50-59,9 ani” | 640+48 = 688 |
| sub 70 de ani | “sub 60 ani” și “60-69,9 ani” | 688 +19 = 707 |
| sub 80 de ani | “sub 70 ani” și “70-79,9 ani” | 707 + 6 =713 |
| sub 90 de ani | “sub 80 ani” și “80-89,9 ani” | 713+1 = 714 |
| mulțimea tuturor valorilor posibile (de regulă, mulțimea numerelor reale) | “sub 80 ani” și “peste 90 de ani” | 714+0=714 |
Similar, se definește seria de frecvențe cumulative descendente, ca fiind setul de frecvențe al claselor definite de fiecare limită și +∞ (sau o valoare finită mai mare decât toate valorile posibile).
Convențional, și la seria de frecvențe cumulative descendente de mai sus, se adaugă efectivul submulțimii definite de valori cuprinse în mulțimea numerelor reale, astfel că majoritatea tabelelor cu serii de frecvențe cumulative vor cuprinde, pentru n limite din interiorul mulțimii de valori posibile
- n+1 intervale pentru clase cu frecvență cumulativă ascendentă (cele cu verde) și
- n+1 intervale pentru clase cu frecvență cumulativă ascendentă (cele cu albastru).
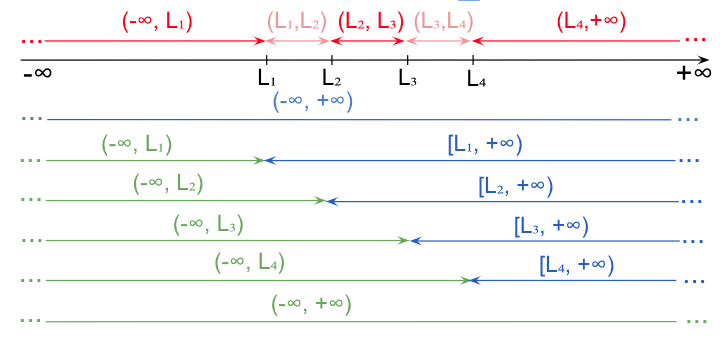
Dacă statisticianul știe cu certitudine că valorile posibile sunt mărginite, poate fi acceptabil ca extremele -∞ și sau +∞ să fie înlocuite cu valorile acestora. De exemplu, pentru notele din catalog, care nu pot fi mai mici de 1 sau mai mari de 10, va fi la fel de corect să definim intervalele astfel:
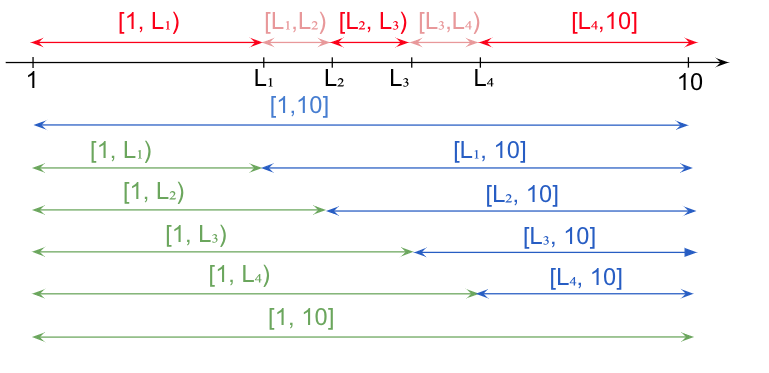
Ca și în cazul seriei de frecvențe ascendente, clasele cu care calculăm frecvențe descendente se pot scrie în două feluri, ca reuniune de grupe (cele cu roșu) sau ca diferență de mulțimi:
| Interval de vârstă (ani) | Grupe de interval componente | Frecvențe absolute cumulative descendente | Construcție echivalentă | Frecvența absolută cumulativă descendentă, calculată ca diferență |
| mulțimea numerelor reale | “sub zero ani”, “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani”, “80-89,9 ani”, “cel puțin 90 ani” | 0 + 62 + 102 + 220 + 167 + 89 + 48 + 19 + 6 + 1 + 0 = 714 | populația | efectivul populației, 714 |
| cel puțin 0 ani | “0-9,9 ani”, “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani” “80-89,9 ani”, “cel puțin 90 ani” | 62 + 102 + 220 + 167 + 89 + 48 + 19 + 6 + 1 + 0 = 714 | “multimea numerelor reale” minus grupa “sub zero” | 714 – 0 = 714 |
| cel puțin 10 ani | “10-19,9 ani”, “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani” “80-89,9 ani”, “cel puțin 90 ani” | 102 + 220 + 167 + 89 + 48 + 19 + 6 + 1 + 0 = 652 | “cel puțin 0 ani” minus grupa “0-9,9 ani” | 714 – 62 = 652 |
| cel puțin 20 ani | “20-29,9 ani”, “30-39,9 ani”, “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani” “80-89,9 ani”, “cel puțin 90 ani” | 220 + 167 + 89 + 48 + 19 + 6 + 1 + 0 = 550 | “cel puțin 10 ani” minus grupa “10-19,9 ani” | 652 – 102 = 550 |
| cel puțin 30 ani | “30-39,9 ani”, “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani” “80-89,9 ani”, “cel puțin 90 ani” | 167 + 89 + 48 + 19 + 6 + 1 + 0 = 330 | “cel puțin 20 ani” minus grupa “20-29,9 ani” | 550 – 220 = 330 |
| cel puțin 40 ani | “40-49,9 ani”, “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani”, “80-89,9 ani”, “cel puțin 90 ani” | 89 + 48 + 19 + 6 + 1 + 0 = 163 | “cel puțin 30 ani” minus grupa “30-39,9 ani” | 330 – 167 = 163 |
| cel puțin 50 ani | “50-59,9 ani”, “60-69,9 ani”, “70-79,9 ani”, “80-89,9 ani”, “cel puțin 90 ani” | 48 + 19 + 6 + 1 + 0 = 74 | “cel puțin 40 ani” minus “40-49,9 ani” | 163 – 89 = 74 |
| cel puțin 60 ani | “60-69,9 ani”, “70-79,9 ani”, “80-89,9 ani”, “cel puțin 90 ani” | 19 + 6 + 1 + 0 = 26 | “cel puțin 50 ani” minus grupa “50-59,9 ani” | 74 – 48 = 26 |
| cel puțin 70 ani | “70-79,9 ani”, “80-89,9 ani”, “cel puțin 90 ani” | 6 + 1 + 0 = 7 | “cel puțin 60 ani” minus grupa “60-69,9 ani” | 26 – 19 = 7 |
| cel puțin 80 ani | “80-89,9 ani”, “cel puțin 90 ani” | 1 + 0 = 0 | “cel puțin 70 ani” minus grupa “70-79,9 ani” | 7 – 6 = 1 |
| cel puțin 90 ani | “cel puțin 90 ani” | 0 | “cel puțin80 ani” minus grupa “80-89,9 ani” | 1 – 1 = 0 |
Din nou, intervalele semimărginite pot fi închise sau deschise:
- Aici, dat find că intervalele sunt închise la marginea lor inferioară, și frecvențele cumulative descendente vor fi definite cu intervale închise la limita finită. Vom scrie [40, ∞), și vom descrie cu “cel puțin 40 de ani”, nu “mai mare de 40 de ani”.
- Dacă intervalele de grupă ar fi fost deschise la limita inferioară ((10,20], (20, 30] etc, având descrierea “0,01-10 ani”, “10,01-20 ani”, “10,01-20 ani”), am fi avut și intervalele pentru frecvențele cumulative descendente deschise la limita finită ((0,∞), (10, ∞), (20, ∞) etc, descrise ca “mai mare de 0”, “mai mare de 10” etc)
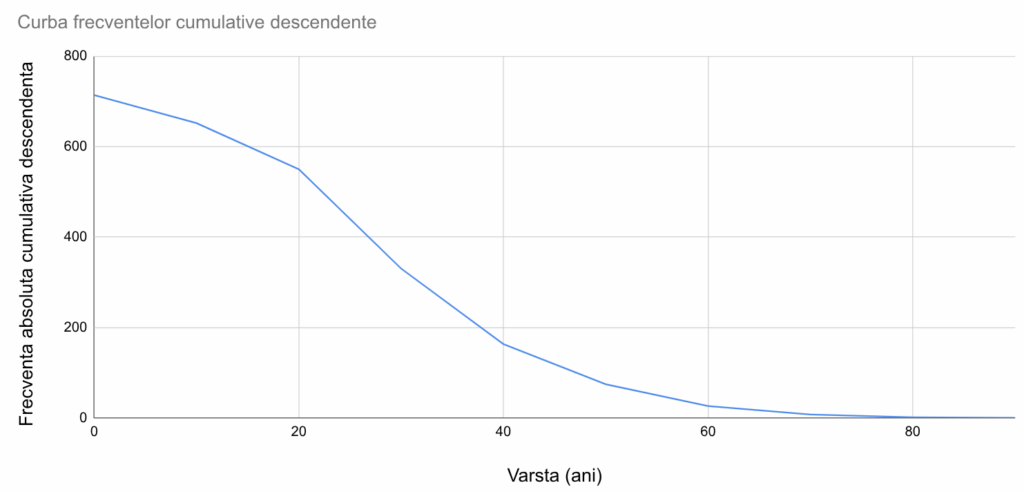
Recapitulând, conform convențiilor, seriile de frecvențe cumulative sunt, pentru n limite din interiorul mulțimii de valori posibile, un grup de n+1 numere, pentru că se includ n intervale de forma (L, +∞) sau (-∞, L), la care se adaugă și mulțimea numerelor reale, cu efectiv egal cu efectivul populației. Aici
- Frecvențe cumulative ascendente sunt 0 (frecvența absolută a primei grupe de interval, “sub zero”), 62, 164, … 714 (calculate din frecvența cumulativă ascendentă precedentă, plus o frecvență de grupă).
- Frecvențe cumulative descendente sunt 714 (efectivul populației), 714, 652, … 1 (calculate din frecvența cumulativă descendentă precedentă, minus o frecvență de grupă).
Probabil ați observat că, pentru n limite interne, vom face n adunări și respectiv n scăderi, deși avem (n+1) intervale de grupă. De asemenea, poate ați observat că în majoritatea cazurilor, o frecvență cumulativă ascendentă este împerecheată cu una descendentă, dar nu și în cazurile în care săgeata verde sau albastră cuprinde întreaga mulțime a numerelor reale. Pentru a rezolva aceste neregularități, unele surse consideră că cele două serii de frecvențe cumulative trebuie completate cu frecvența mulțimii vide, zero. Prin adăugarea mulțimii vide, putem spune că și muțimea numerelor reale are o pereche. Această completare este cu certitudine necesară graficelor din următoarea secțiune, și poate apărea în surse neobișnuite (de exemplu, ChatGPT).
Se pot calcula, prin împărțire la efectivul colectivității, și frecvențe relative cumulative descendente sau ascendente:
| Interval de vârstă (ani) | Frecvențe absolute cumulative ascendente | Frecvențe relative cumulative ascendente |
| sub 0 ani | 0 | 0 / 714 ≈ 0 |
| sub 10 ani | 62 | 62 / 714 ≈ 0.087 |
| sub 20 de ani | 164 | 164 / 714 ≈ 0.23 |
| sub 30 de ani | 384 | 384 / 714 ≈ 0.538 |
| sub 40 de ani | 551 | 551 / 714 ≈ 0.772 |
| sub 50 de ani | 640 | 640 / 714 ≈ 0.896 |
| sub 60 de ani | 688 | 688 / 714 ≈ 0.964 |
| sub 70 de ani | 707 | 707 / 714 ≈ 0.99 |
| sub 80 de ani | 713 | 713 / 714 ≈ 0.999 |
| sub 90 de ani | 714 | 714 / 714 = 1 |
| mulțimea tuturor valorilor posibile | 714 | 714 / 714 = 1 |
La fel ca frecvențele absolute cumulative, putem calcula frecvența relativă, fie ca sumă a multor frecvențe de grupă, fie din frecvența cumulativă vecină. Astfel, frecvența relativă cumulativ ascendentă pentru “sub 40 de ani” (aici, 551/714) poate fi
- suma frecvențelor relative de interval pentru sub 0 ani (0), 0-9,9 ani (62/714), cea pentru 10-19,9 ani (102/714), cea pentru 20-29,9 ani (220) și cea pentru 30-39,9 ani (167/714)
- suma frecvențelor relative de interval pentru “sub 30 de ani” (384/714) și cea pentru 30-39,9 ani (167/714).
Convenția de scriere abreviată a frecvențelor cumulative
Din păcate, în manualele de economie, frecvențele cumulative vor fi mai frecvent enumerat lângă grupele de interval, fără o etichetă descriptivă:
| Interval de vârstă (ani) | Frecvențe absolute de grupă | Frecvențe absolute cumulative ascendente | Frecvențe absolute cumulative descendente |
| 0-9,9 | 62 | 62 | 714 |
| 10-19,9 | 102 | 164 | 652 |
| 20-29,9 | 220 | 384 | 550 |
| 30-39,9 | 167 | 551 | 330 |
| 40-49,9 | 89 | 640 | 163 |
| 50-59,9 | 48 | 688 | 74 |
| 60-69,9 | 19 | 707 | 26 |
| 70-79,9 | 6 | 713 | 7 |
| 80-89,9 | 1 | 714 | 1 |
În această situație, fiecare frecvență cumulativă va corespunde celui mai îngust interval de la infinit (-∞ la frecvențe ascendente, +∞ la frecvențe descendente) ar cuprinde intervalul de pe acea linie. De exemplu
- 384 este o frecvență cumulativă ascendentă care corespunde celui mai îngust interval de frecvență ascendentă (deci de la -∞) și include grupa “20-29,9 ani”. Este vorba de intervalul (-∞, 30), care va fi descris cu “sub 30 de ani”.
- În dreptul său, 550 este o frecvență cumulativă descendentă care corespunde celui mai îngust interval de frecvență ascendentă (deci de la +∞) și include grupa “20-29,9 ani”. Este vorba de intervalul [20,+∞), care va fi descris cu “cel puțin 20 de ani”.
Graficul ogivă
În graficul ogivă, reprezentăm grafic fiecare frecvență cumulativă împreună cu semnificația ei. Astfel, 163 este numărul de persoane cu vârsta “cel puțin 40”, așa că vom pune un punct la poziția (40, 163). Împreună cu punctele similare (50, 74), (60, 26), etc vom obține o curbă a frecvențelor descendente:
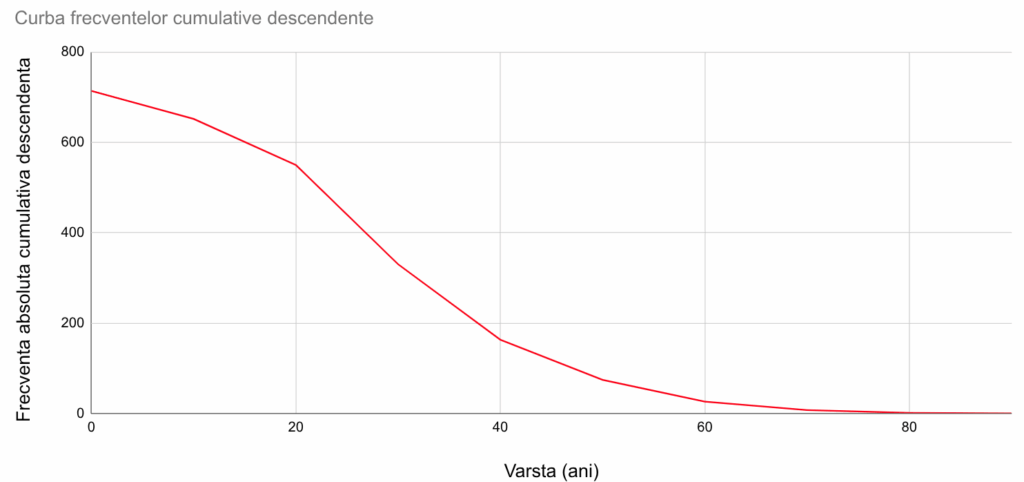
În acest exemplu, pentru curba similară a frecvențelor ascendente, va fi necesară o aproximare. De exemplu, 640 este frecvența absolută cumulativă ascendentă pentru vârste de sub 50 de ani. Aici, “sub 50 de ani” reprezintă intervalul (-∞, 50), a cărui limită superioară este practic egală cu 50. Prin urmare, vom reprezenta această frecvență cu punctul de coordonate (50, 640) chiar dacă, tehnic, poziția ar trebui să fie la un x infinitezimal mai mic de 50. Împreună cu (40, 551), (30, 384) etc, vom crea o curbă a frecvențelor ascendente:
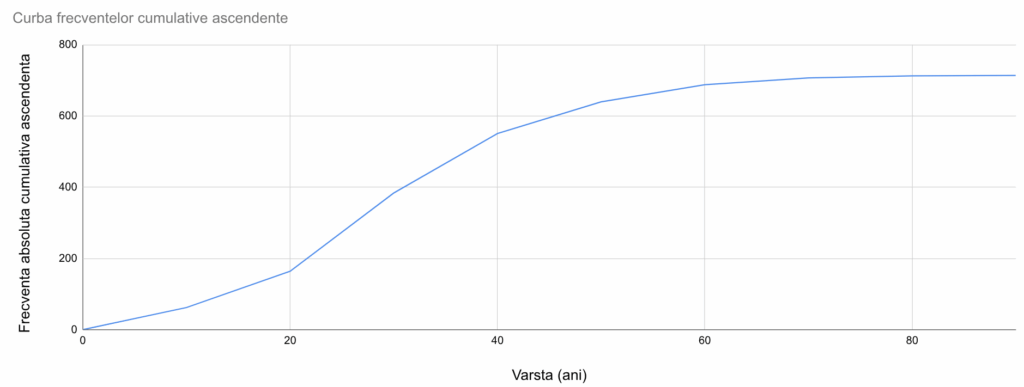
Ambele curbe trebuie să atingă y=0 și y=N (efectivul colectivității).
- Dacă tabelul-sursă este scris în convenția economiștilor, cu includerea unei mulțimi ce acoperă toate valorile posibile (de exemplu, mulțimea numerelor reale), va exista cu certitudine un punct de coordonată y=N. Va trebui însă să îi alegeți, oarecum arbitrar, o poziție pe axa x. (“Mulțimea numerelor reale” nu conține un număr, în contrast cu celelalte descrieri de interval de frecvență cumulativă.) Dacă se cunoaște o limită certă a valorilor, se poate folosi aceasta. Dacă nu, vedeți următoarea secțiune.
- Dacă seria de frecvențe cumulative este scrisă în convenția economiștilor, cu cel mai mic număr egal cu frecvența absolută a primei grupe, există posibilitatea să nu aveți nici un punct pentru y=0. Cu certitudine, un punct cu y=0 trebuie folosit, și va fi adăugat la nevoie, listei de puncte, sub forma mulțimii vide. Dar nici acest punct nu va avea un x cert, și vor trebui folosite metode de aproximare ca mai sus.
Suprapunerea celor două curbe de frecvențe cumulative este numită graficul ogivă, deoarece va mima forma detaliului arhitectural omonim:
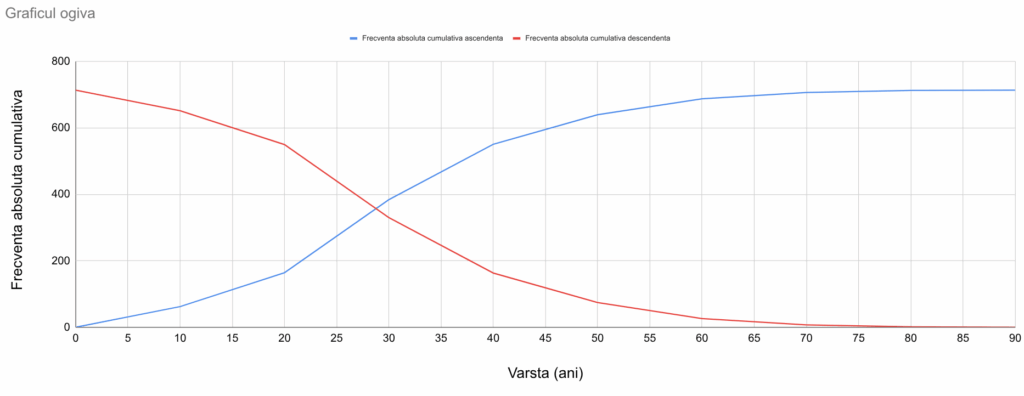
În preajma limitei de 29 de ani, numărul de pasageri cu vârstă mai mică decât limita devine egal cu numărul de pasageri cu vârstă mai mare decât limita.
