Grupare după variabilă calitativă cu variabile dihotomice ajutătoare
Această secțiune demonstrează, în trei variante, modul de calcul al frecvențelor relative și absolute în Excel.
Vom începe în maniera cea mai simplă, mai potrivită pentru limbaje de programare de ordin general, cu un fișier similar cu care am demonstrat discretizarea cu variantă în afara ordinii, modificat pentru a nu fi afectat de diferențele de separator zecimal:
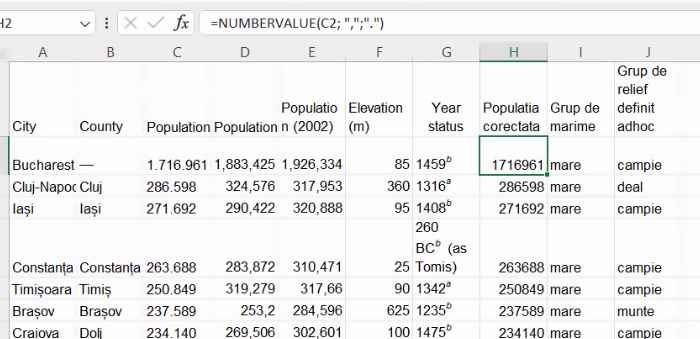
Reamintim formula de calcul a coloanei de grupă de relief:
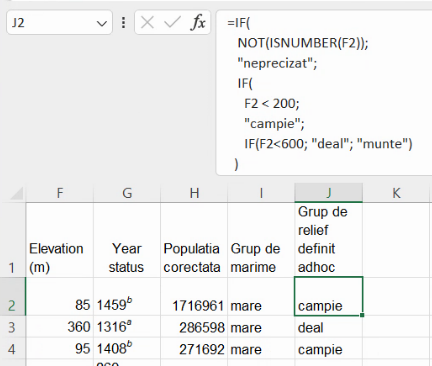
Vom adăuga câte o coloană surogat pentru fiecare din valorile posibile ale coloanei J.
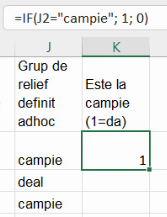


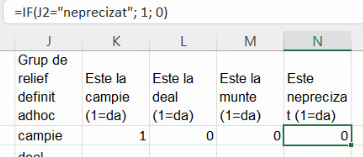
Extindem formulele până la baza tabelului.
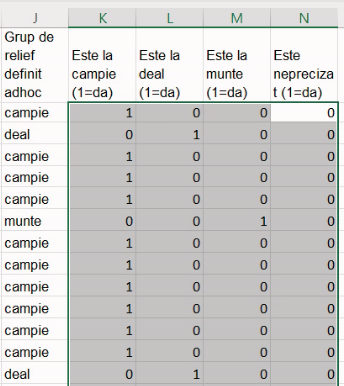
Așa cum am menționat în secțiunea despre prelucrare primară, suma pentru fiecare această coloană surogat este chiar efectivul grupei (frecvența absolută), iar media fiecărei coloane este proporția (frecvența relativă). Prin urmare, putem construi un tabel cu următoarele formule:
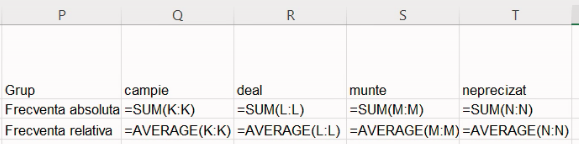
Puteți trece de la afișarea rezultatelor la afișarea formulelor și invers cu Ctrl+`. Întorcându-ne la rezultate, vom obține tabelul ce combină seria de distribuție pe frecvențe absolute, cu seria de distribuție pe frecvențe relative:
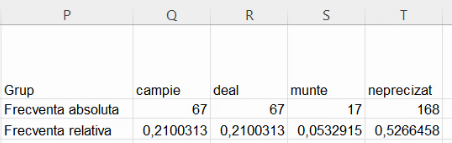
Deci, din localitățile tabelate, 168 nu au altitudine precizată, ceea ce constituie o proporție de cca 52,7% din colectivitate. Dacă preferăm frecvențele procentuale selectăm frecvențele relative subunitare, și selectăm una din opțiunile Percent.
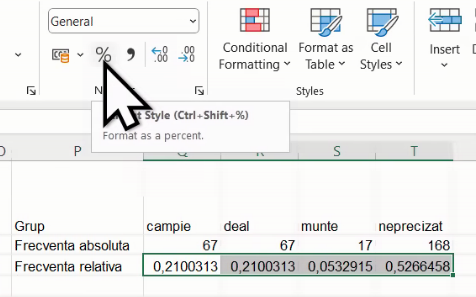
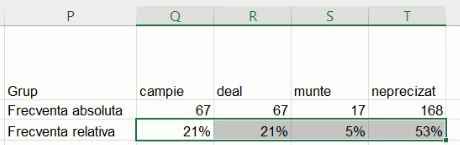
În acest exemplu, frecvențele relative procentuale au aparent suma de 99% din cauza lipsei zecimalelor.
O a doua metodă de generare a seriei de distribuție este cea în care Excel va genera automat toate teste logice folosite în coloana surogat, va atribui 0 sau 1 fiecărei celule testate la fel ca în coloana surogat, și va returna direct suma acestor valori surogat.
Funcția COUNTIF() primește două argumente, o regiune din Excel și un așa-numit criteriu. În forma sa cea mai intuitivă, criteriul este o porțiune dintr-un test logic, ca de exemplu, “>0”, caz în care valoarea din fiecare celulă din regiune va fi juxtapusă criteriului. De exemplu, COUNTIF(A1:A9, “>100”) va crea testele A1>100, A2>100, … A9>100, va proba valoare de adevăr pentru fiecare, și va returna numărul de cazuri în care condiția este adevărată.
Dacă criteriul nu cuprinde un operator de comparație, Excel va prezuma semnul de egalitate. COUNTIF(A1:A9, 5) va returna numărul de propoziții adevărate din setul A1=5, A2=5 … A9=5. Cu parametru alfanumeric, COUNTIF(A1:A9, “5”) va returna numărul de propoziții adevărate din setul A1=”5″, A2=”5″, … A9=”5″. Un test mai simplu decât cel de mai sus care verifică dacă “Abrud” se află în celulele A1:A100 va fi IF(COUNTIF(A1:A100, “Abrud”) > 0, “gasit”, “negasit”).
Dacă criteriul este complet absent, Excel va prezuma că acesta este “=0”.
Să recreăm gruparea descrisă în secțiunea despre prelucrare primară, conform căreia localitățile mai mari de 50 de mii de locuitori sunt “mici”, cele peste 200 de mii sunt “mari”, și restul “mijlocii”. Cu ajutorul COUNTIF(), vom obține direct seria de distribuție cu frecvențe absolute:
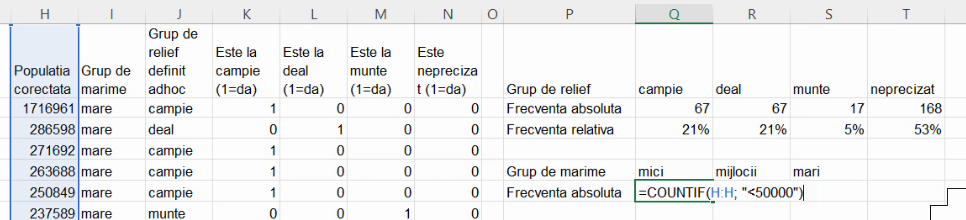
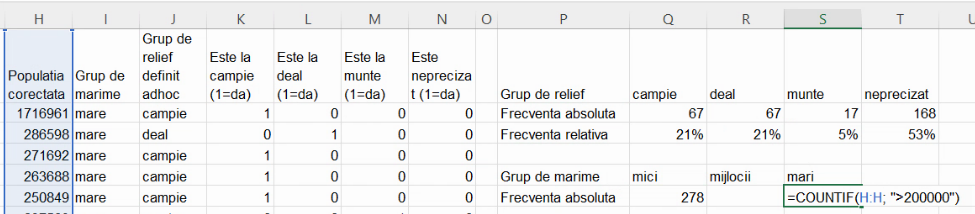
Pentru grupa de localități de mărime mijlocie, vor fi necesare două teste la nivelul fiecărei valori. COUNTIF() nu va mai fi suficient.
Funcția COUNTIFS() primește un număr par de argumente. Fiecare pereche de argumente este similară celor folosite de COUNTIF(). Este necesar ca toate regiunile să aibă aceeași dimensiune, deoarece Excel va parcurge simultan toate regiunile-argument. De exemplu, în imaginea de mai sus, COUNTIFS(I:I, “mare”, J:J, “deal”) va crea și evalua simultan câte o celulă din fiecare regiune. Condiția I1=”mare” va fi testată în pereche cu J1=”deal”; condiția I2=”mare” va fi testată în pereche cu J2=”deal”; etc. COUNTIFS va returna numărul de perechi (triplete etc), pentru care toate testele sunt satisfăcute (în acest exemplu, numărul de localități mari de deal).
Vom calcula frecvența relativă pentru grupa de mărime mijlocie cu COUNTIFS():
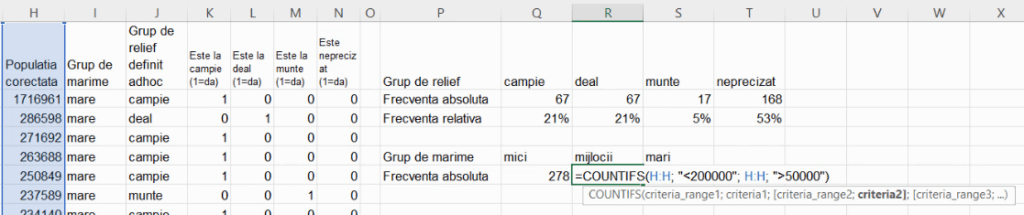
Pentru a calcula frecvențele absolute, este necesar efectivul colectivității, car eva fi suma frecvențelor absolute ale grupelor.

Frecvențele relative vor fi obținute prin împărțirea frecvențelor absolute la efectivul colectivității:

Am putea încerca să extindem formula pentru frecvențe relative în celelalte două celule, însă rezultatul nu va fi cel scontat:
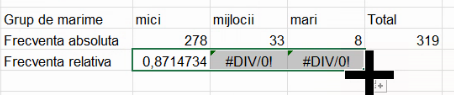
Erorile sunt cauzate de faptul că, la extinderea la dreapta, și numitorul și numărătorul sunt mutate la dreapta:

Este de dorit ca numărătorul să se modifice la fiecare coloană, însă este necesar ca numitorul să rămână T6. Pentru a preveni modificarea literei în U6, V6 etc, este necesară blocarea literei cu prefixul $ (dolar):

Acum putem extinde formula fără a pierde numitorul:
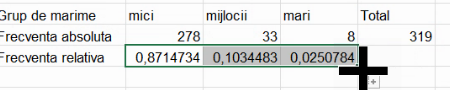
Putem verifica numitorul din celelalte celule:

Deci, conform aceste clasificări ad hoc, în România sunt 8 localități mari (de peste 200 de mii), respectiv o proporție de cca 0,025 din efectivul colectivității:

Un fișier cu aceste serii de distribuție se găsește aici.
Grupare după variabilă calitativă cu PivotTable
Maniera modernă de construire a seriilor de distribuție, PivotTable, a fost inspirată de un grup de metode frecvent folosite de sumarizare a bazelor de date, numit OLAP (Online Analytical Processing). În acel context, pivotarea însemna trecerea de la diversele modalități de a sumariza datele de afaceri (de exemplu, tabel pe grupe de vârstă ale clientului, pe regiuni, pe dealeri etc.).
În Excel, PivotTable este o metodă de a obține date sintetice (efective, medii, minime, maxime etc) despre o serie de date stocată sub forma convențională, cu unitățile statistice pe linii și variabilele pe coloane. În plus, este necesar ca prima linie a serie de date să aibă numele variabilelor (nu date).
Vom începe din nou cu fișierul cu care am demonstrat discretizarea cu variantă în afara ordinii, modificat pentru a fi agnostic la setările separatorului zecimal . Verificați că setările computerului la care lucrați au păstrat caracterul numeric al coloanei H, și calculele din coloana J s-au efectuat corect:
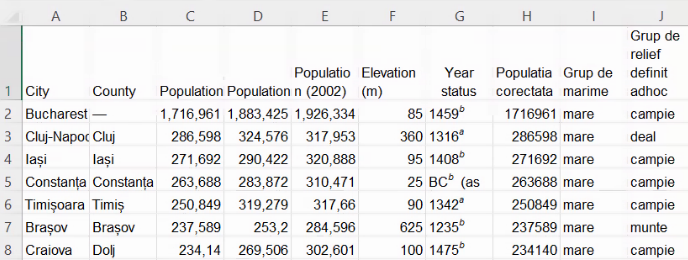
Vom selecta toate coloanele deja existente, și vom alege butonul PivotTable din Insert. Dialogul care apare solicită adresa unde va crea tabelul nou. E ideal să folosiți o altă foaie de calcul.
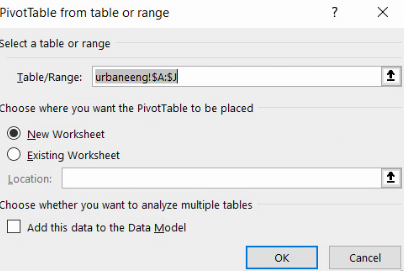
Inițial tabelul nu are conținut, dar în partea dreaptă a foii de calcul ar trebui să apară opțiunile pentru acest tabel. Să începem prin a crea un tabel care conține seria de distribuție pe forme de relief, fiecare grupă pe câte o linie. Vom trage din lista de variabile pe cea numită “grupe de relief” până în cutia destinată liniilor (Rows) tabelului pivot:
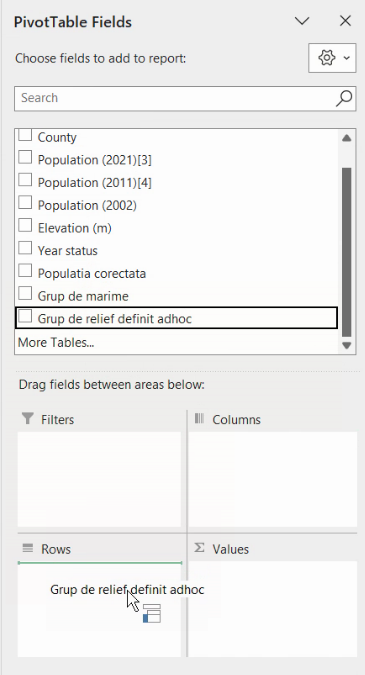
Dacă ați reușit să plasați variabila în lista Rows, tabelul pivot va fi actualizat automat să arate valorile unice ale variabilei cu care vom face gruparea. Totuși, tabelul nu are conținut.
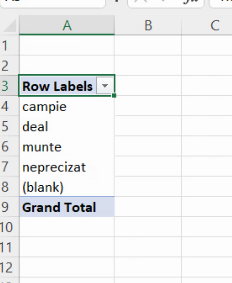
Pentru o serie de distribuție, este suficient să numărăm (Count) valorile din orice coloană cu date complete, întrucât PivotTable va aplica echivalentul lui COUNT() sau COUNTA(). Deci, pentru a adăuga conținut tabelului, vom trage variabila completă City (coloana A, care conține numele localităților) peste regiunea Values:
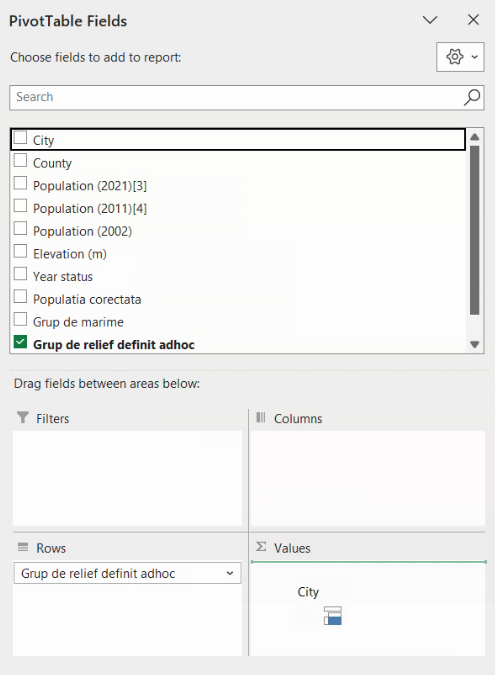
La eliberarea butonului mausului, City va fi adăugat la lista Values, cu denumirea “Count of City”:
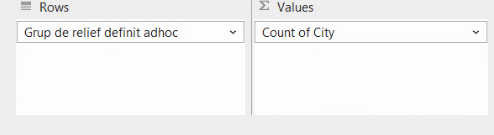
Iar tabelul va fi actualizat, pentru a afișa efectivele fiecărei grupe, și deci seria de distribuție:

Motivul pentru care City a devenit “Count of City” este că, implicit, PivotTable va calcula COUNTA() (numărul de celule nonvide) pentru coloane cu conținut alfanumeric, și SUM() pentru coloane cu conținut numeric. De exemplu, dacă vom trage și coloana cu Populația (numeric) în regiunea Values, vom obține și suma populațiilor.
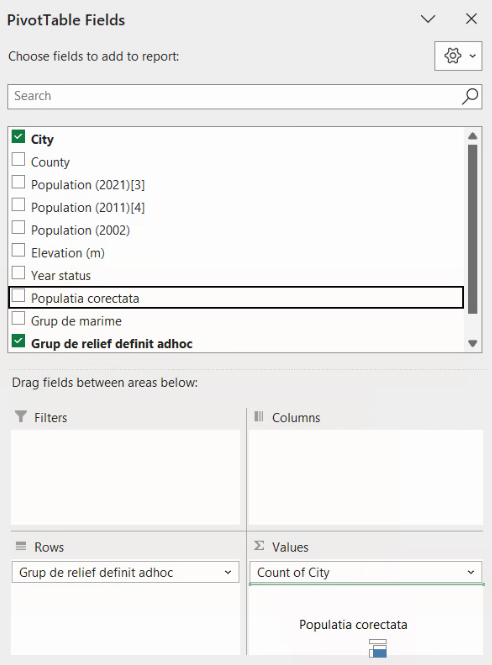


Deci, cele 17 localități de “munte” (cu altitudine peste 600 m) au împreună 490,343 locuitori.
Mai mult, în loc de sumă, putem calcula alte caracteristici ale grupei, precum minim, maxim etc. cu click pe dropdownul de lângă variabilă, așa cum este ea listată în Values:
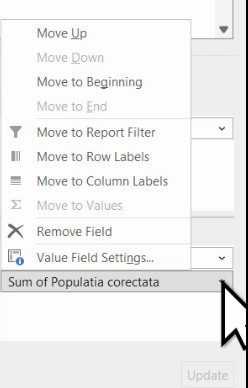
Am eliminat Suma populațiilor pe grupe, pentru a mai modifica caracteristicile seriei de distribuție.
Din dropdownul de lângă titlul primei coloane a tabelului de distribuție, putem alege să ascundem unele valori. Cel mai frecvent vom ascunde “(blank)”, adică, aici, liniile fără conținut în coloana “Grupă de relief”.
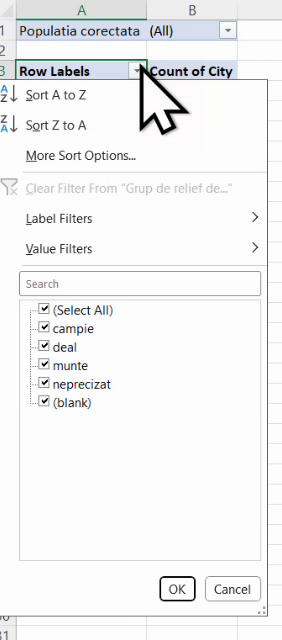
Pentru calculul frecvențelor relative, mai tragem o dată variabila City în regiunea Values:
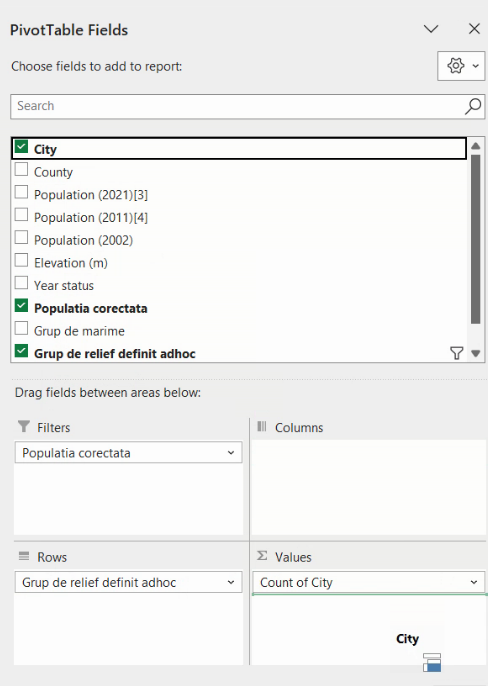
Inițial vom produce un duplicat al coloanei deja existente:
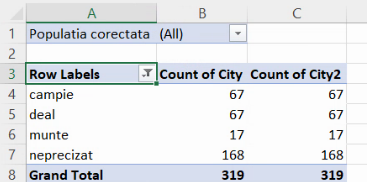
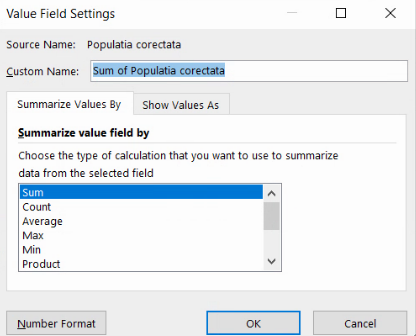
Deschidem Value Field Settings pentru noua coloană din seria de distribuție:
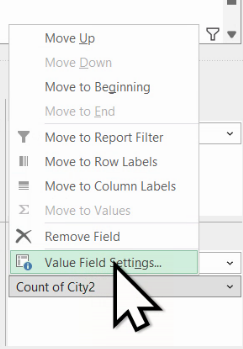
Vom folosi tabul Show Values As.
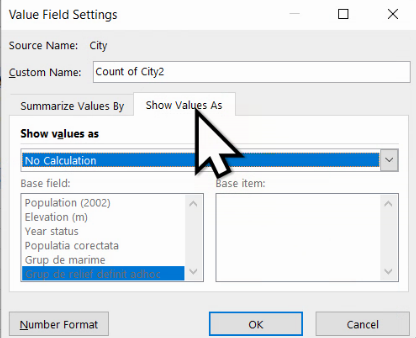
Din dropdownul Show values as, alegem % of Column Total:
Astfel, am obținut și seria de distribuție cu frecvențe relative:
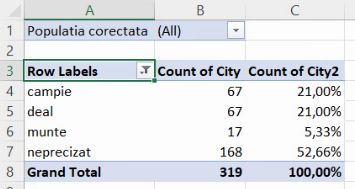
Rezultatul PivotTable se află în fișierul acesta.
Tabel de contingență
Tabelul de contingență sumarizează distribuția unei colectivități, când două metode distincte de grupare sunt posibile.
Să reluăm fișierul cu care am demonstrat discretizarea cu variantă în afara ordinii, cu modificare pentru independență de setările pentru separator zecimal. Din nou, asigurați-vă că valorile din coloana H sunt numerice, iar calculele din coloana J s-au efectuat corect.
Și data aceasta, selectăm toate coloanele din seria de date, alegem Insert – PivotTable, cerem ca noul tabel să fie creat într-o foaie de calcul nouă. Din nou, tragem Grupa de relief la Rows și City la Values.
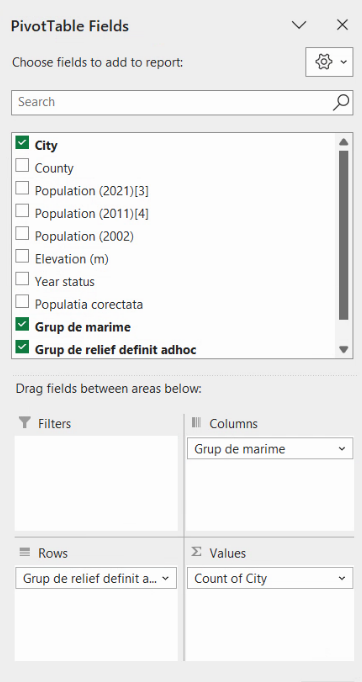
Rezultatul va fi un tabel care descrie modul în care se împarte populația după două metode de grupare independente, adică un tabel de contingență:
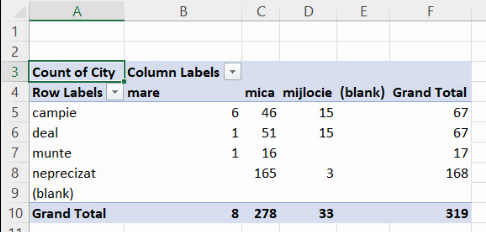
De exemplu, sunt 6 localități mari de câmpie, sunt 51 localități mici de deal etc. Tabelul de contingență devine mai lizibil după ascunderea opțiunii “(blank)“, ca mai sus, și prin afișarea explicită a lui zero în celulele fără conținut:
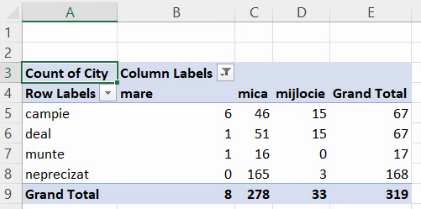
Pentru un tabel de contingență care combină o grupare pe 3 grupe (mică / mijlocie / mare) cu una pe 4 grupe (câmpie / deal / munte / neprecizat), vom avea de descrie 3×4 =12 submulțimi. În tabelul de contingență de mai sus, acestea sunt descrise de celulele B5:D8. În contextul unui tabel de contingență, cele 12 frecvențe absolute (6, 46, 15, 1, …) se numesc și efective parțiale. Suma tuturor efectivelor parțiale este egală cu efectivul populației.
La capătul fiecărei linii se află un total de linie. De exemplu, pe linia dedicată localităților de munte, suma efectivelor parțiale 1, 16 și 0 este, conform ultimei coloane, 17. Numerele de pe ultima coloană, (67, 67, 17, 168), sunt chiar seria de distribuție a localităților pe forma de relief, obținută în exemplul din secțiunea precedentă. În contextul unui tabel de contingență, aceste totaluri se mai numesc și efective marginale.
Similar, la capătul fiecărei linii, dacă am activat opțiunea de afișare a totalului, vom regăsi un alt set de efective marginale, (8, 278, 33). Ca și în cazul celorlalte efective marginale, este vorba chiar de seria de distribuție pe mărime, întrucât 8 localități ar fi mari, 33 – mijlocii și 278 – mici. Suma efectivelor parțiale, suma efectivelor marginale însumând linii, suma efectivelor marginale însumând coloane și efectivul populației sunt egale.
Vom folosi aceste frecvențe absolute pentru a calcula trei tipuri de frecvență relativă. Cea mai utilă este frecvența relativă parțială. Aici, vom descrie fiecare submulțime (de exemplu, localități mari de câmpie) ca proporție din efectivul colectivității, aici B5/E9:
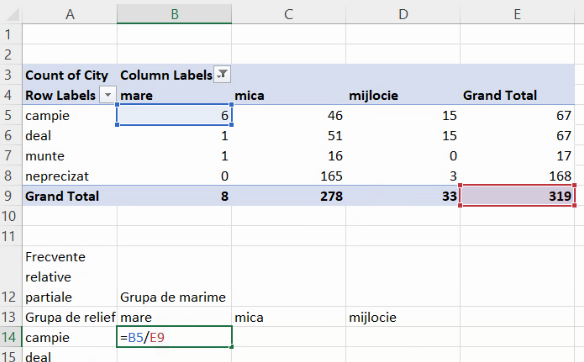
Deficiența acestei formule este inabilitatea sa de a se extinde în lateral sau în jos. Am arătat mai sus că, pentru a extinde o formulă lateral, dar a păstra neschimbate una sau mai multe litere desemnând coloane, este necesară blocarea literei cu prefixul dolar. Aici, vom dori trecerea de la 6/319 la 46/319, 15/319, ceea ce înseamnă că vom bloca numai litera pentru numitor:
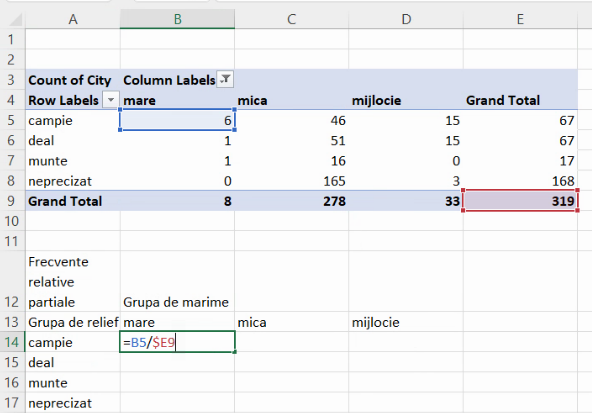
Formula se extinde fără probleme lateral:
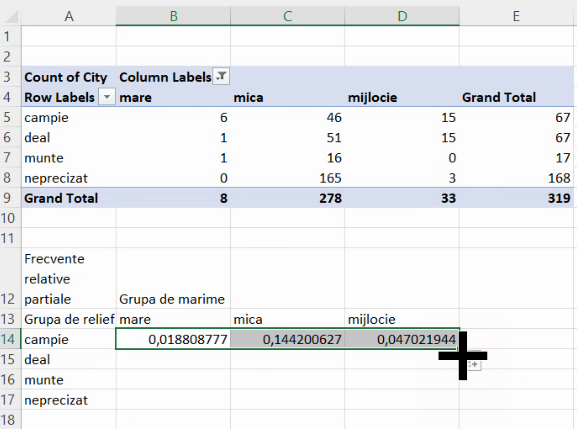
Putem verifica că numitorul rămâne valoarea din E9:
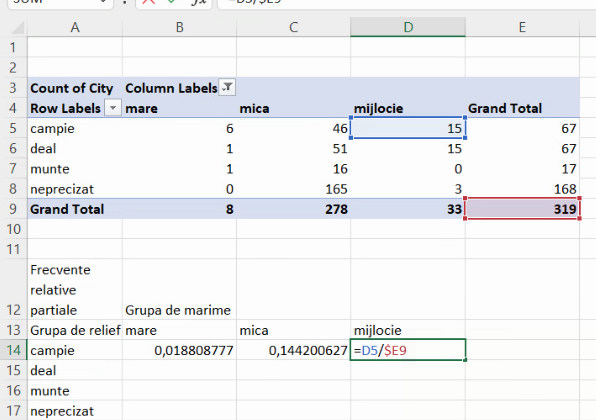
Însă extinderea în jos va duce la formule eronate:
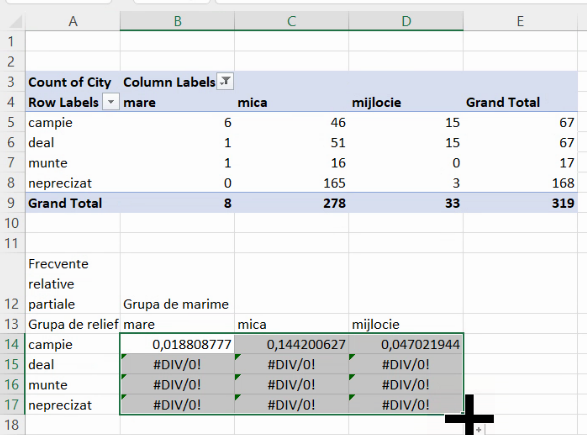
Putem verifica conținutul acestor formule eronate, astfel observând că extinderea în jos a dus la modificarea numărului de linie și pentru numitor și pentru numărător:
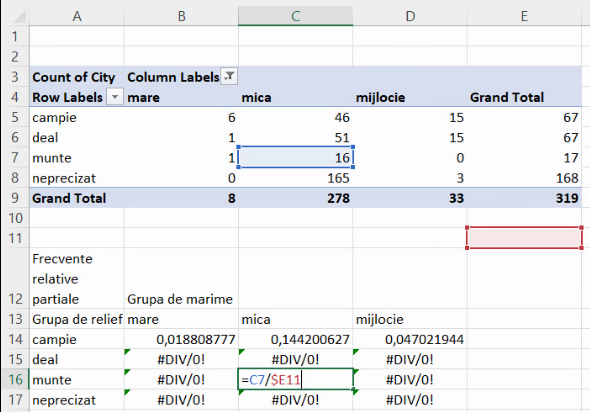
Pentru ca împărțirile să nu se facă și la E10, E11, E12, va fi necesar ca, încă de la prima formulă, să blocăm și numărul de linie al numitorului tot cu prefixul dolar:
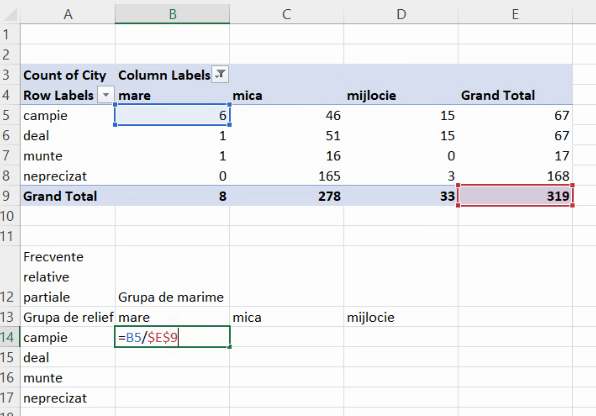
Extindem la dreapta și în jos:
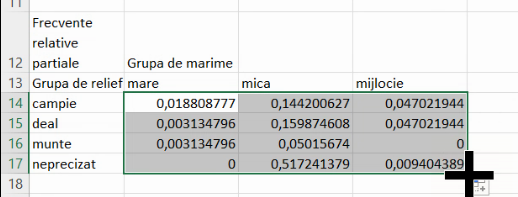
Putem verifica blocarea numărătorului inspectând celulele nou completate:
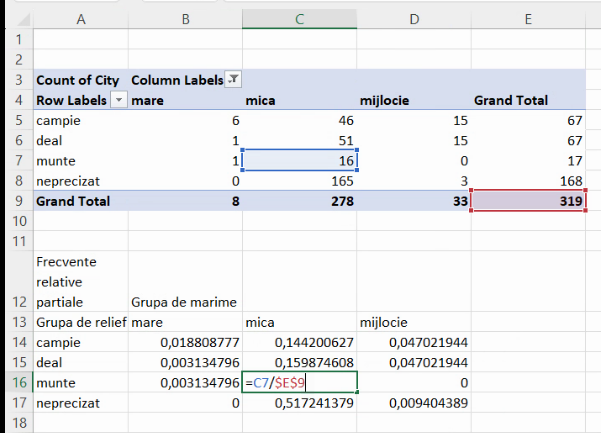
Un indiciu (nu o dovadă) că acestea sunt frecvențele relative parțiale corecte este testarea sumei lor, de exemplu cu Quick stats de pe bara inferioară:
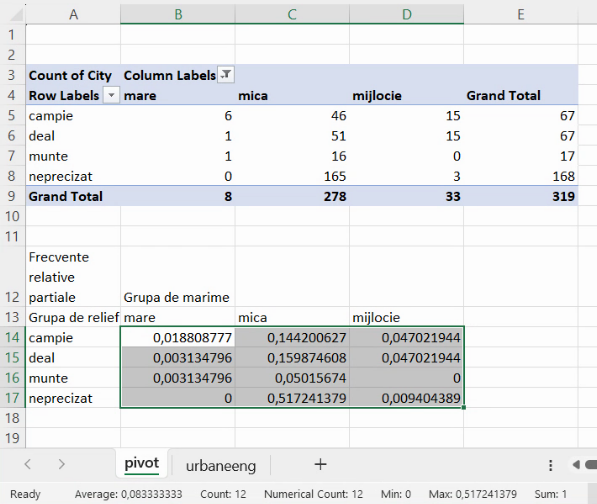
Frecvențele relative marginale sunt sumele frecvențelor relative parțiale, fie pe o linie, fie pe o coloană:
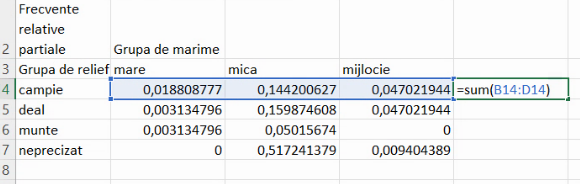
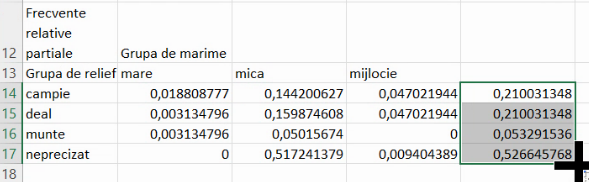
Ca și în cazul efectivelor marginale, frecvențele relative marginale creează o serie de distribuție. Aici, (0,21; 0,21; 0,053; 0,526) sunt chiar seria de distribuție a localităților pe forme de relief, calculată în secțiunea precedentă.
O frecvență relativă marginală poate fi calculată fie ca sumă a acelei lini (sau coloane), fie ca raport al efectivului marginal corespunzător din tabelul de contingență cu frecvențe absolute, împărțit la efectivul colectivității. Aici, valoarea din E17, descriind proporția de localități cu relief neprecizat, este fie suma numerelor de pe acea linie (0+0,517+0,09), fie raportul efectivului parțial al acelorași localități cu relief neprecizat (168) la efectivul colectivității (319).
Putem completa tabelul și cu frecvențele relative marginale care însumează coloane:

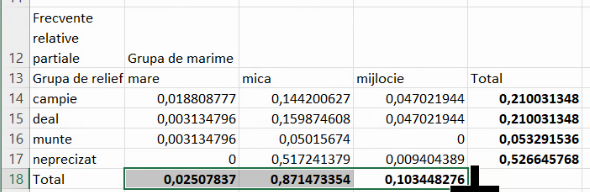
Suma tuturor frecvențelor relative marginale de un anumit tip (fie de linie, fie de coloană) este 1, ceea ce se poate verifica cu Quick Stats de pe bara inferioară:
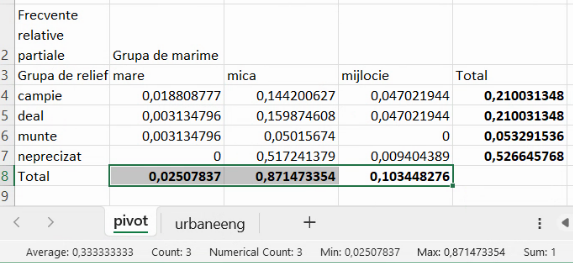
Celelalte două tipuri de frecvență relativă sunt cele condiționate. Frecvențele relative condiționate de forma de relief sunt cele care exprimă proporții în interiorul fiecărei grupe de formă de relief. De exemplu, frecvența relativă condiționată de relief a localităților mari de câmpie redă proporția ocupată de cele 6 localități mari de câmpie în interiorul grupei lor de relief (localități de câmpie, frecvență absolută 67):
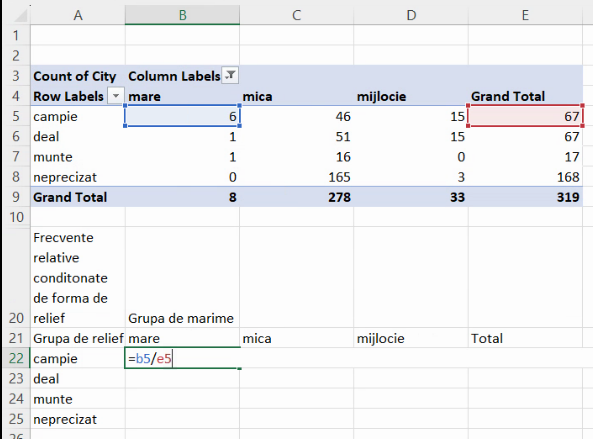
Din nou, vom avea de împărțit numerele din regiunea B5:D8 la numere repetate. Astfel:
- frecvența relativă condiționată de relief a localităților mici de câmpie este 46/67
- frecvența relativă condiționată de relief a localităților mijlocii de câmpie este 15/67
cu același numitor, 67 (E5).
Pe alte linii, proporțiile sunt, de exemplu:
- frecvența relativă condiționată de relief a localităților mari de munte este 1/17
- frecvența relativă condiționată de relief a localităților mici de munte este 16/17
- frecvența relativă condiționată de relief a localităților mijlocii de munte este 0/17
din nou cu același numitor, de data aceasta alt efectiv marginal, 17 (E7).
În concluzie, o formulă adecvată extinderilor va fi cea care permite schimbarea numărului de linie, dar nu permite schimbarea literei de coloană:
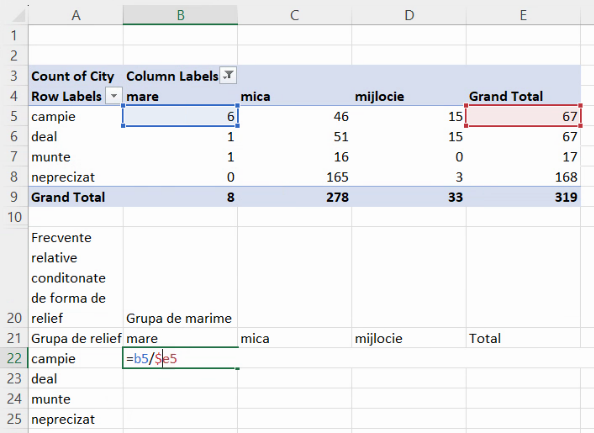
Extindem formula în jos și la dreapta. Putem verifica numărătorul celulelor nou completate, demonstrând că la extindere s-au folosit numărătorul și numitorul dorite:
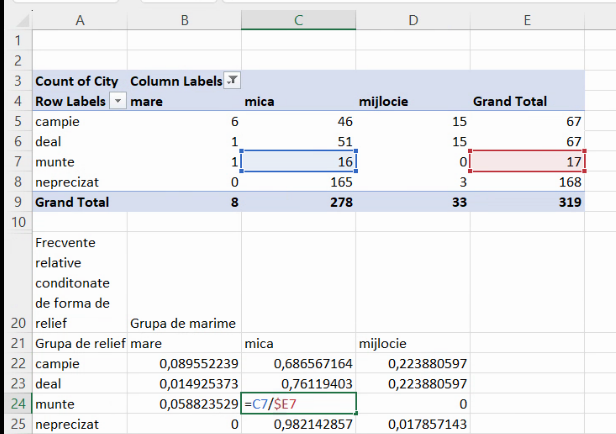
La acest tabel, nu sunt necesare totaluri de linie sau coloană. Deoarece procentele sunt calculate în interiorul grupei descrise de o linie, frecvențele relative condiționate de variabila de pe linie constituie câte o serie de distribuție. De exemplu, (0,089; 0,686, 0,223) descriu repartiția localităților de câmpie în subgrupele (“mare”, “mica”, “mijlocie”), iar suma lor va fi 1. Pe de altă parte, suma valorilor de pe coloanele acestui tabel nu are sens.
Se mai pot defini și frecvențe relative condiționată de cealaltă metodă de grupare, aici condiționată de grupa de mărime. În acest caz, toate proporțiile vor fi definite în interiorul aceleiași grupe de mărime. De exemplu, frecvența relativă condiționată de grupa de mărime a localităților mari este proporția, din grupa localităților mari (efectiv 8), reprezentată de localități mari de câmpie. În acest caz, vom dori ca numitorul să fie unul din efectivele marginale însumând coloane (8, 278, sau 33), ceea ce înseamnă că numărătorul trebuie să se schimbe liber în cursul extinderilor, însă linia numitorului trebuie să rămână 9. Vom bloca linia cu prefixul dolar:
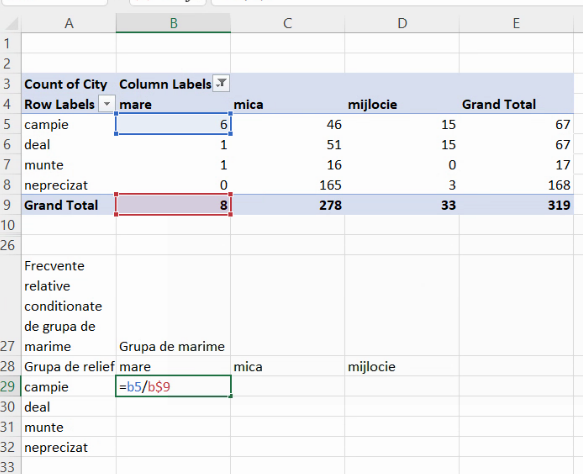
Extindem formula:
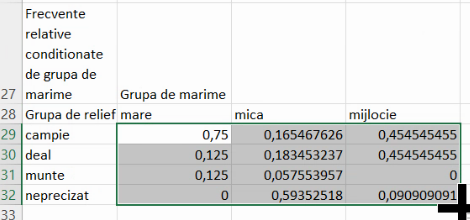
Deci, din grupul de localități mijlocii, o proporție de cca. 0,0909 (sau “9,09%”, dacă o formă procentuală este necesară) sunt cu altitudine neprecizată; etc. În acest nou tabel de contingență cu frecvențe relative condiționate, fiecare coloană constituie o serie de distribuție în interiorul respectivei grupe de mărime, și are deci suma 1. Suma pe linie nu are sens.
Un fișier cu toate aceste tabele se găsește aici.
Reprezentarea grafică a seriei de distribuție pe grupe descrise de una sau două variabile calitative
Vom începe cu un fișier care cuprinde ambele tabele pivot din exemplele anterioare. Pentru a crea un grafic cu coloane, am putea selecta o parte din datele din PivotTable, apoi Insert – Chart – 2-D column – Clustered column (primul buton de sub 2-D):
Motivul pentru care voi evita această abordare este că, deși grafic rezultat este perfect, rapiditatea metodei nu lasă loc de explicații. Atunci când un PivotTable este folosit ca sursă pentru un grafic, Excel va crea un grafic la fel de sofisticat, numit PivotChart:
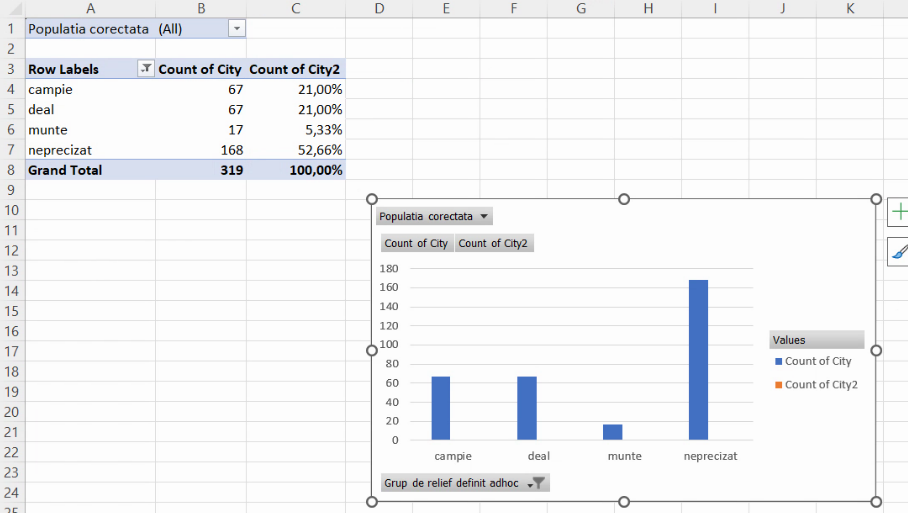
Pentru o demonstrație mai clară, voi crea un grafic obișnuit. Voi începe prin a copia datele din PivotTable alături:
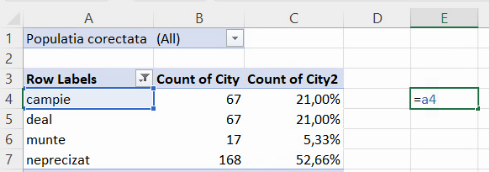
Extindem formula în jos și la dreapta:
Punem etichete noului tabel:
Selectăm noul tabel și solicităm din nou Insert – Chart – 2-D Column – Clustered column:
Click pe acel buton va produce un grafic de structură relativ complet:
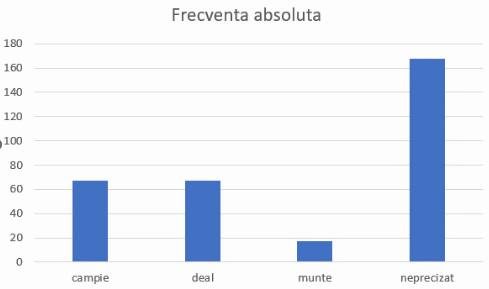
Pentru a fi complet, este necesară doar adăugarea de titluri de axă. Orice element tipic al unui grafic din Excel se adaugă cu Add chart element din Chart design:

Ajustăm titlul:
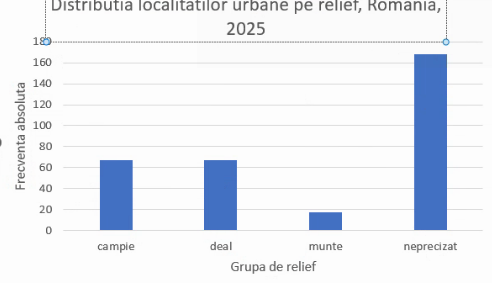
O serie de elemente necesare acestui grafic ce descrie o structură de populație au fost alese automat și merită evidențiate ca alegeri optime, Astfel, descrierile de coloană (labels) sunt la mijlocul coloanei, și nu avem linii de rețea (gridlines) paralele cu coloanele și nici marcaje (ticks) pe axa ce enumeră grupele. Avem linii de rețea perpendiculare pe coloane, ceea ce ne ușurează comparațiile vizuale, și chiar calculele. De exemplu, cea mai înaltă coloană are marginea superioară între linia pentru 160 și cea pentru 180, relativ la mijlocul acelui spațiu, sugerând o valoare a frecvenței absolute pentru grupa cu relief neprecizat de cca. 170 (media celor două numere anterioare).
Pentru tabelul de contingență există mai multe opțiuni de ilustrare grafică. Vom începe cu frecvențele absolute (efectivele parțiale). Le vom copia alături, pentru a evita situația în care Excel construiește un PivotChart:
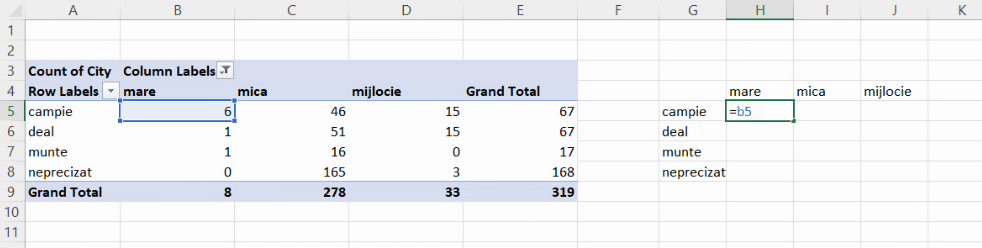
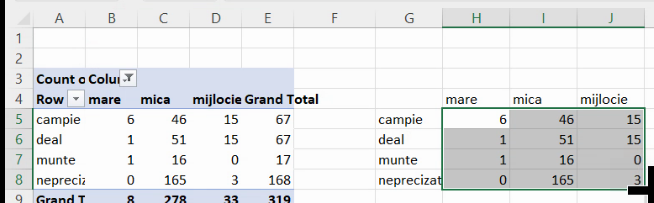
Selectăm noul tabel și alegem din nou Insert – Chart – 2-D column – Clustered column:
Rezultatul este un grafic cu coloane neetajat, în care fiecare grupă de mărime este indicată cu o culoare specificată în legendă și cu fiecare grupă de relief indicată prin proximitate geometrică (spații mai mici în interiorul grupei decât între grupe):
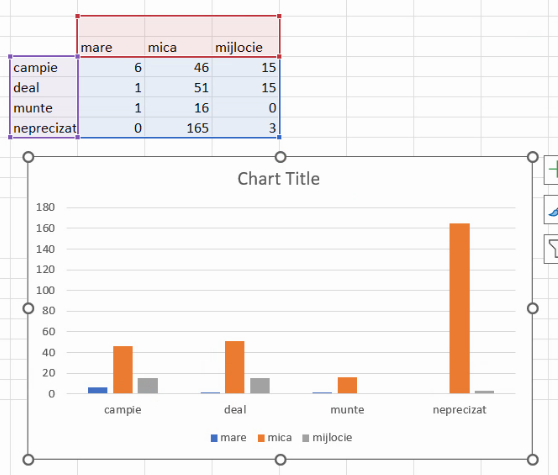
Din nou, sunt necesare titluri pentru axe și pentru grafic, de exemplu:
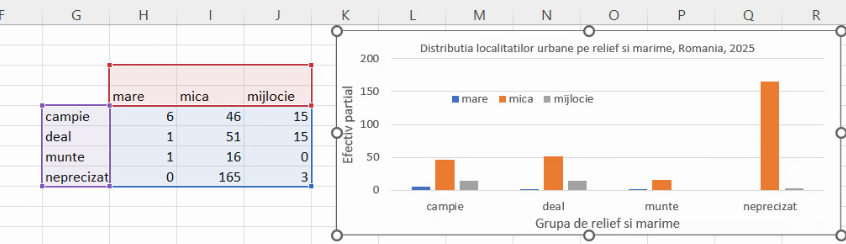
Acest grafic permite multe comparații vizuale, inclusiv unele mai puțin necesare (“localitățile mici de câmpie sunt ma multe decât localitățile mari de deal”). Alternativa mai utilizat[ este etajarea coloanelor din acest grafic. Selectăm din nou tabelul cu date copiate, și folosim Insert – Chart – 2-D column – Stacked column (al doilea buton):
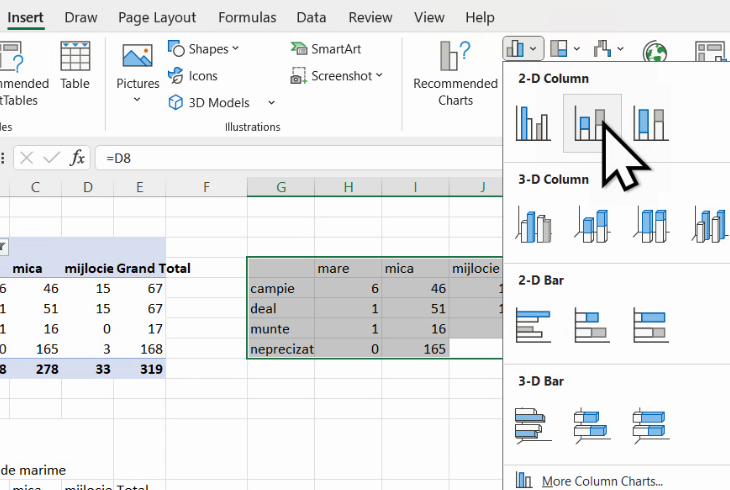
Rezultatul este din nou cvasicomplet, cu excepția titlurilor:
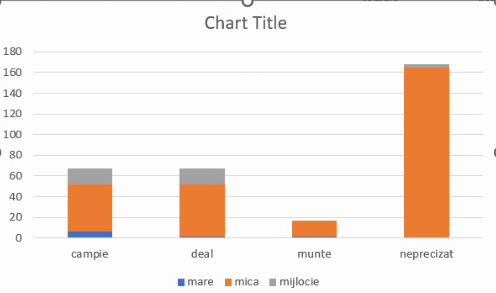
Putem adăuga titluri, ca de exemplu:
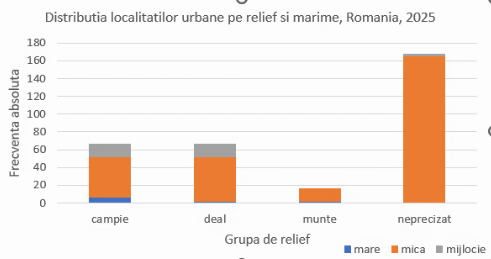
Frecvențele relative parțiale sunt proporționale cu efectivele parțiale, și deci un grafic bazat pe ele, fie el cu coloane simple sau cu coloane etajate, va arăta identic ca proporții:

Mai util este graficul cu frecvențe pațiale condiționate, dacă am plasat datele în Excel astfel încât suma pe fiecare linie să fie 1, ceea ce va face barele etajate să aibă lungimea egală. Aici, fie folosim frecvențele relative condiționate de relief. Selectăm acel tabel și alegem din nou Insert – Chart – 2-D column – Stacked column:
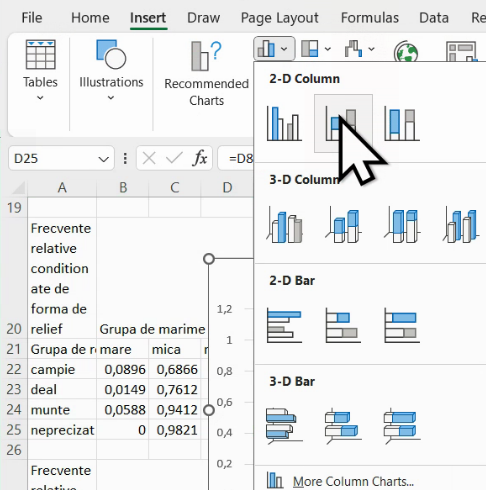
Vom obține un set de coloane de înălțime egală a căror utilitate este că ne permite comparația distribuțiilor în interiorul fiecărei grupe:
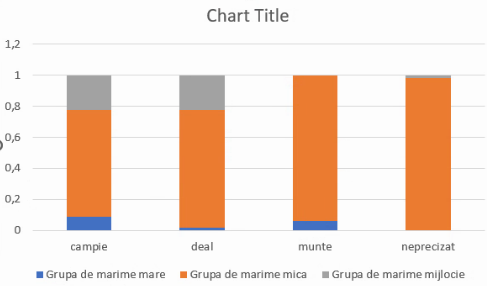
Acest grafic ne permite să afirmăm că proporția localităților mari este cea mai mare în grupa de câmpie, și cea mai mică în grupa de altitudini neprecizate. Acest grafic permite comparația între frecvențe relative. Graficele precedente ne permiteau comparații vizuale între frecvențe absolute (“numărul localităților mari este cel ma mare în grupa de câmpie”).
Pentru completitudine, vom pune titluri axelor și graficului:
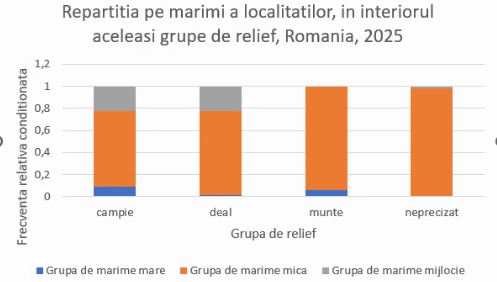
Întrucât aceste coloane au precis 1, nu este necesară extinderea axei ordonate mai sus de 1. Pentru a modifica o limită a axei, selectăm axa, de exemplu cu dropdownul din Format Chart:
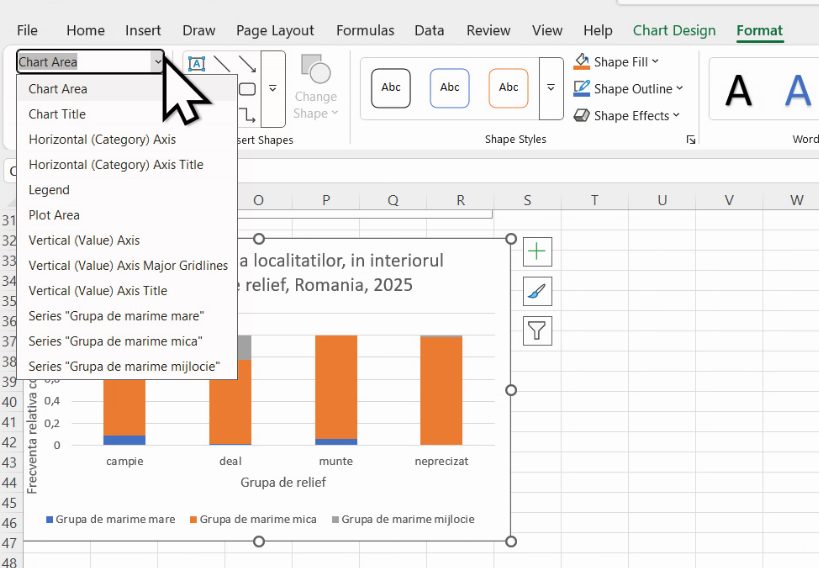
(Este necesar ca graficul sau o componentă a sa să fie selectată,pentru ca meniul Format chart să devină vizibil.) Vom selecta axa ca atare:
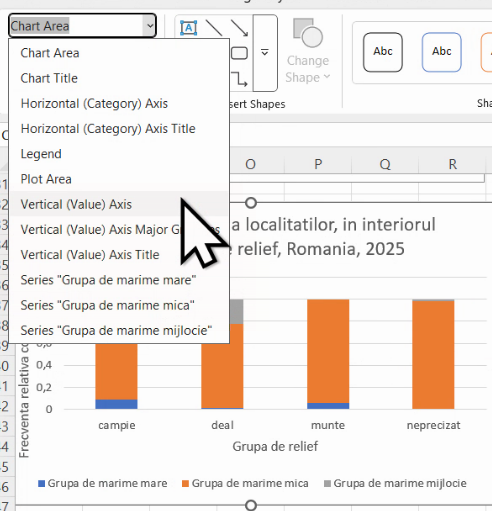
Menoul din stânga ferestrei Excel va deveni Format axis:
Alegeți butonul Axis Options (al patrulea) de sub tabul Axis Options:
Desfășurați opțiunile de sub “> Axis options”, pentru a accesa valorile minimă și maximă ale axei. Introduceți 1:
Rezultatul va fi modificarea axei ordonatei:
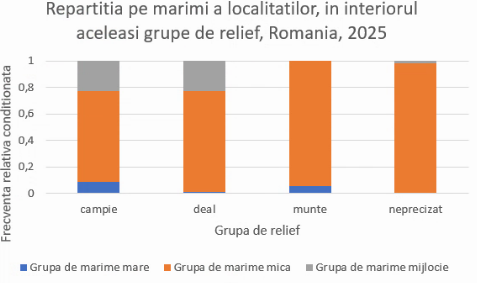
Un fișier cu aceste grafice se află aici.
Grupare pe interval pe baza unei variabile cantitative
Vom începe cu un fișier în care am obținut o coloană cantitativă, numerică, a populației fiecărei localități urbane din România, în manieră agnostică față de setările computerului. Metodele folosind variabile dihotomice sau COUNTIF() / COUNTIFS() sunt practic identice cu cele din secțiunile identice și nu vor fi detaliate aici.
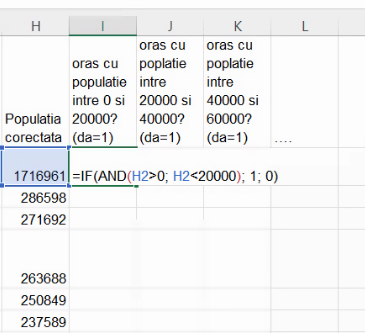

În locul acestor vom folosi funția FREQUENCY() în cele două variante ale sale, pre-2020 și post-2020.
Funcția FREQUENCY(), în ambele sale variante, are două argumente, un set de valori numerice pe care le va grupa, și un set de limite pe care le va folosi în grupare. Un set de n limite desparte mulțimea numerelor naturale în n+1 intervale, și deci =FREQUENCY({1,2,3,4,11,12,20,21,34},{10,20,30}) va returna frecvențele absolute al grupelor definite de intervalele (-∞, 10), [10,20), [20,30), și [30,+∞), respectiv 4, 3, 1, 1. Intervalele sunt închise inferior.
Prin urmare, va fi necesar să pregătim un set de limite pentru a preciza al doilea argument al funcției FREQUENCY, Vom grupa localitățile din România după populație, pe intervale de lățime 20 de mii, adică 0-20 mii, 20-40 mii, 40-60 mii etc.

În varianta pre-2020, funcția FREQUENCY() era numită funcție CSE, deoarece introducerea sa într-o celulă trebuia urmată de combinația de taste Ctrl+Shift+Enter. Motivul pentru care acestă combinație înlocuia tastarea unui simplu Enter este că o funcție CSE returnează mai multe numere, în mai multe celule consecutive. În documentația pre-2020, astfel de funcții care returnează mai multe numere simultan se numea array function. Pentru introducerea corectă a unei funcții CSE; este necesar să precedem introducerea funcție cu selectarea celulelor în care vom obține valorile, începând de la celula de sus, unde vom introduce numărul:
| Așa nu | Așa da |
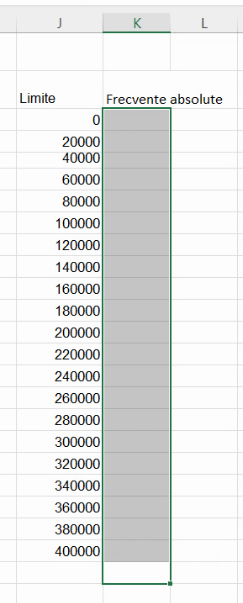 | 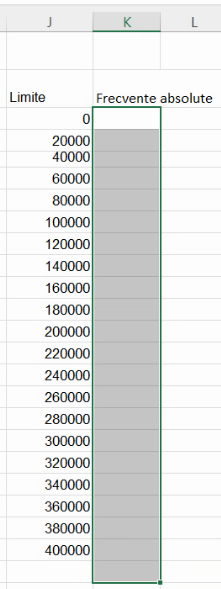 |
Fără a modifica selecția, tastăm formula
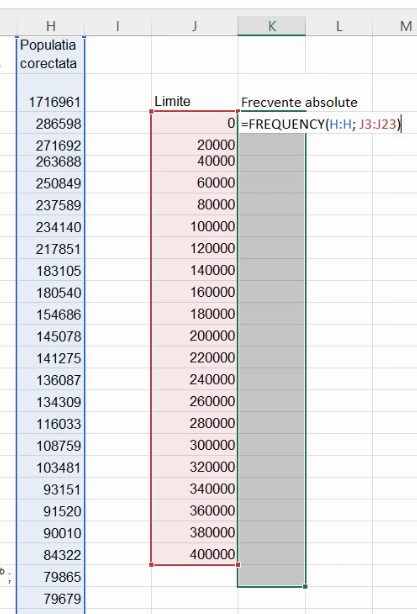
Finalizăm formula cu Ctrl+Shift+Enter, ceea ce va duce la obținerea tuturor frecvențelor absolute, în celulele selectate.
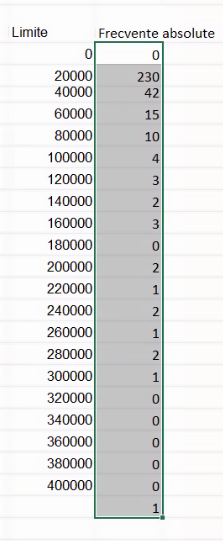
Ca indicator al modalității diferite de introducere a formulei, veți observa că formula a fost încadrată în acolade:
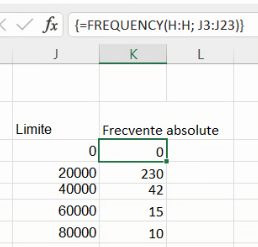
Formula funcției CSE este simultan în toate celulele în care se găsesc rezultatele ei:
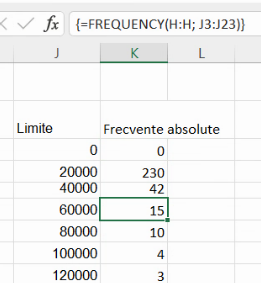
Post-2020, pe lângă funcțiile array (zise funcții CSE), s-au introdus funcțiile dynamic array, care se introduc cu Enter și nu mai necesită preselecția regiunii dorite pentru rezultat. Diferența funcțională este că, așa cum sugerează numele, funcțiile dynamic array își modifică valorile și chiar numărul de celule ocupate cu valori returnate, la fiecare schimbare a celor două regiuni-argument. (Funcțiile CSE trebuiau reintroduse dacă numărul de limite era modificat, și deci regiunea în care rezultatul său trebuia afișat trebuia mărită / micșorată.
Astfel, post-2020, vom introduce aceeași formulă, și vom tasta Enter la finalul ei.
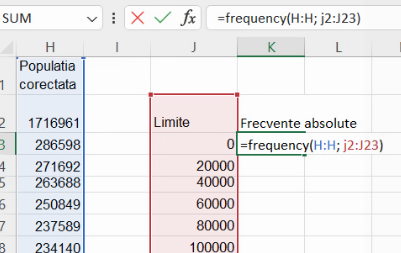
Rezultatul este identic vizual, în ceea ce privește celulele:
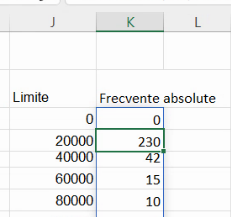
În cazul dynamic array formulas, formula cu FREQUENCY() se regăsește ca atare, fără acolade în celula în care a fost introdusă:
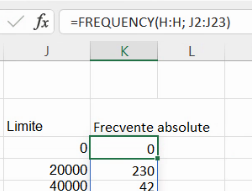
Celelalte celule ale rezultatului lui FREQUENCY() în variantă dynamic array conțin doar o mențiune a formulei-sursă, care nu poate fi editată:
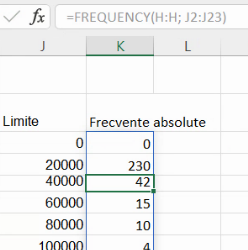
Regiunea ocupată de rezultate unei funcții dynamic array se numește spilled array, în contrast cu rezultatul unei funcții array, care se numește static array.
Indiferent de metoda de definire, tabelul rezultat nu poate fi publicat ca atare. Sunt necesare descrieri ale intervalelor cu care acestea au fost create, respectiv (-∞, 0], (0, 20000], (20000, 40000] etc. Copiem frecvențele absolute din coloana K în coloana N, cu formule. Primul interval este deschis la marginea superioară și deci poate fi denumit “mai mic sau egal cu 0” :
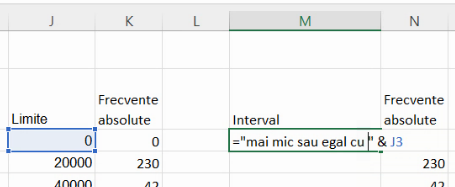
Următoarele intervale au două limite, și se descriu cu “între X și Y”. Pentru că intervalele sunt de forma (X, Y], închise numai superior, vom folosi X+1 în locul lui X.
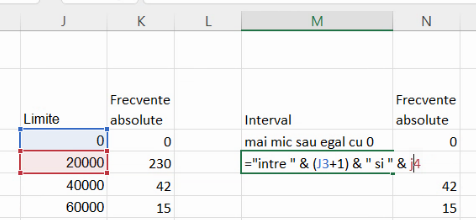
Putem extinde această formulă până la penultimul interval:

Ultimul interval este deschis la limita inferioară X, și poate fi descris cu “mai mult de X”:

În comunicațiile cu publicul larg, unele din intervale pot fi șterse sau comasate, inclusiv cel pentru localități cu populație negativă, și cele cu frecvențe nule. În cele ce urmează
- vom prelua seria de distribuție de mai sus, cu excepția grupei “mai mic de zero”
- vom înlocui limita inferioară a valorilor posibile pe -∞ cu 0
- prin urmare, vom elimina 0 din lista limitelor interne.
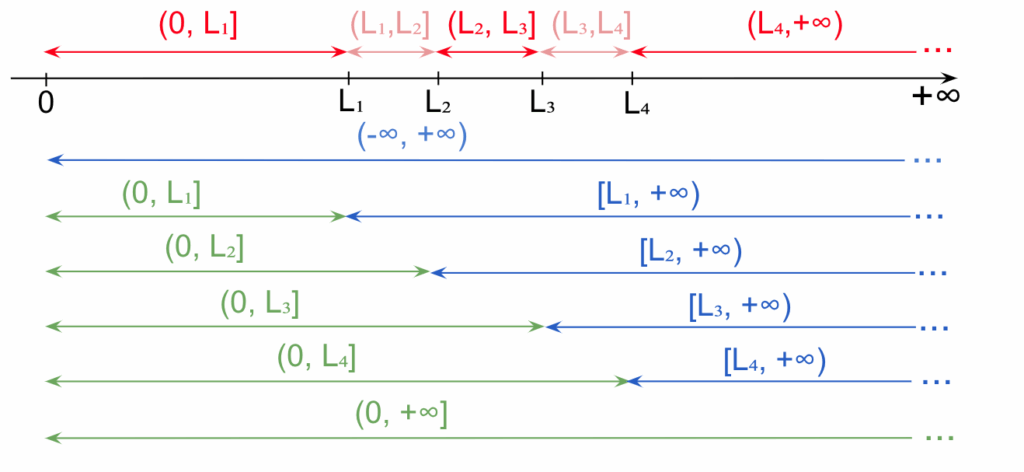
În loc de intervale pentru frecvențe cumulative ascendente de la -∞, așa cum am folosit în capitolul precedent, vom folosi intervale de la 0. Întrucât FREQUENCY() analizează intervale închise la limita superioară (de exemplu (20000, 40000]), vom avea
- intervale închise pentru frecvențele cumulative ascendente, ca (0, 20000], (0, 40000] etc, pe care le vom descrie “cel puțin 20000”, “cel puțin 40000” etc
- intervale deschise pentru frecvențele cumulative ascendente, ca (20000, +∞], (40000, +∞) etc, pe care le vom descrie “mai puțin de 20000”, “mai puțin de 40000” etc
Vom începe prin a copia cu formule tabelul de distribuție produs de FREQUENCY(), în foaia nouă numită “distributii”.
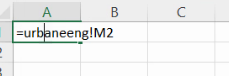
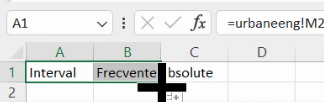
Omitem prima frecvență absolută generată de FREQUENCY():
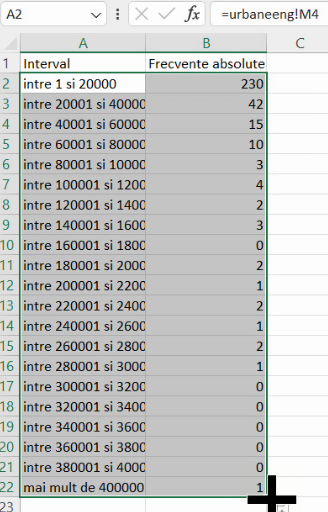
Vom construi tabele de frecvențe cumulative în maniera convențională a economiștilor, cu n intervale interne delimitând n+1 intervale de frecvență cumulativă, incluzând mulțimea tuturor numerelor posibile (liniile verde și albastră fără pereche din diagrama de mai sus), dar fără mulțimile vide care le-ar fi complementul.
În acest aranjament, primul interval pentru frecvență cumulativă ascendentă este identic cu prima grupă. Acesta se definește cu prima limită internă:
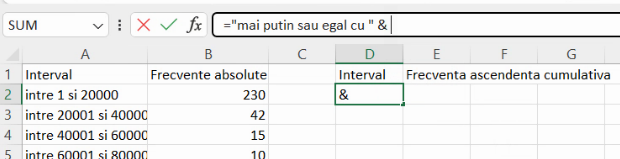




Toate celelalte frecvențe cumulative ascendente sunt calculate prin adunarea unei frecvențe de grupă la frecvența cumulativă precedentă:
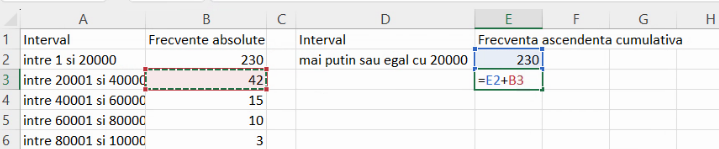


Pentru definiții, putem extinde și formula care calculează definițiile intervalelor:
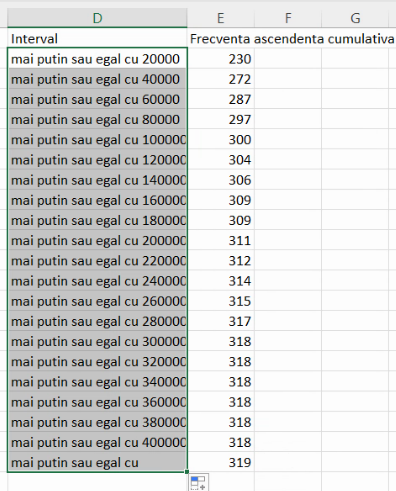
În ultima linie, formula pentru descriere nu mai poate fi introdusă cu aceeași formulă. Acest 319 este suma tuturor frecvențelor de grupă adică este efectivul populației. Intervalul de valori ale populației care i-ar corespunde este mulțimea tuturor valorilor posibile, aici (0, ∞). Spre deosebire de exemplul din capitolul precedent, folosim (0, ∞), ca mulțime a tuturor valorilor posibile, conform indicației din seria de distribuție:
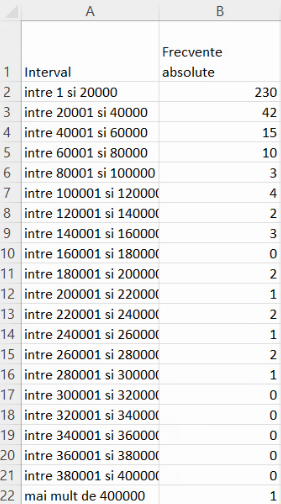
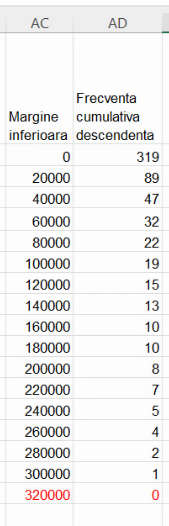
În concluzie, seria frecvențelor cumulative ascendente va fi descrisă, în convenția economiștilor, de tabelul:
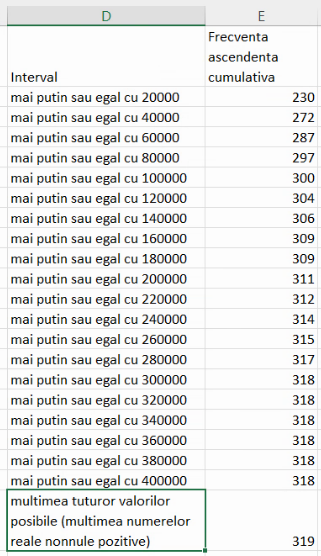
Pentru seria de frecvențe cumulative descendente, se începe cu efectivul colectivității, care, din nou, corespunde intervalului de valori posibile pentru populații ale localităților:
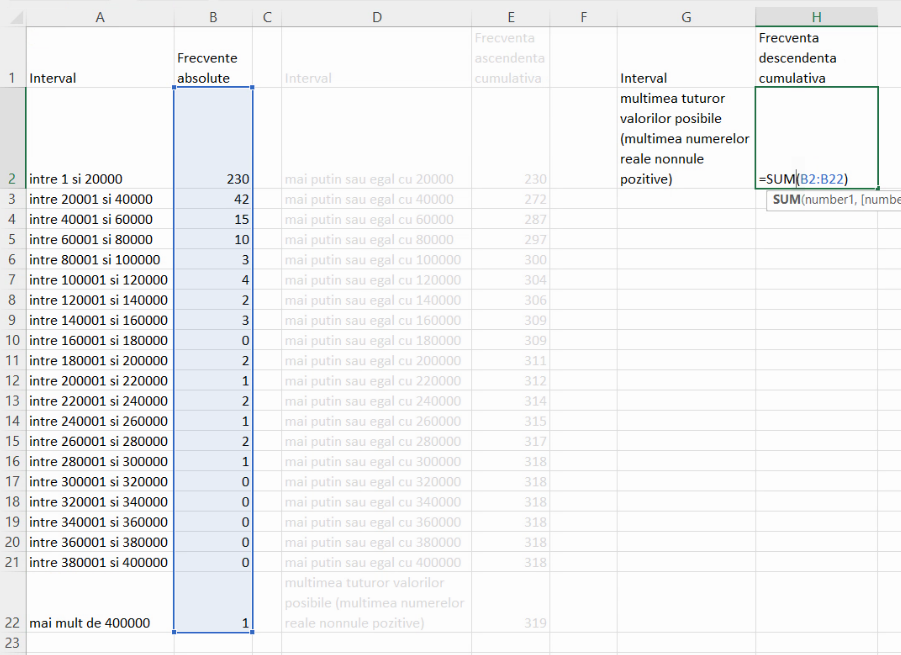
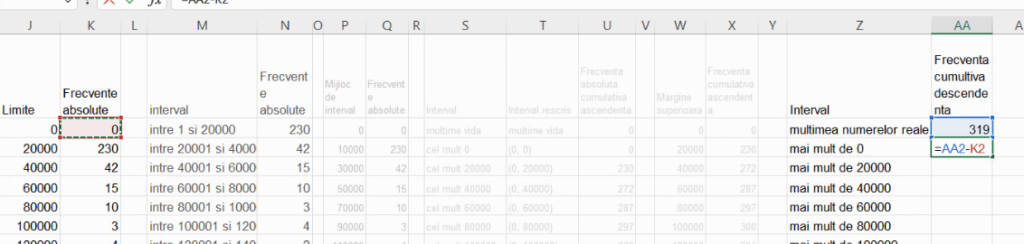
Următoarele frecvențe cumulative descendente se calculează prin scăderea, din frecvența cumulativă descendentă precedentă, a unei frecvențe de grupă:
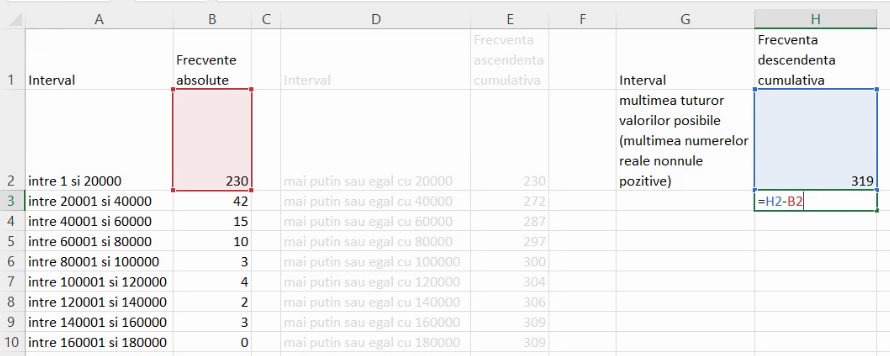
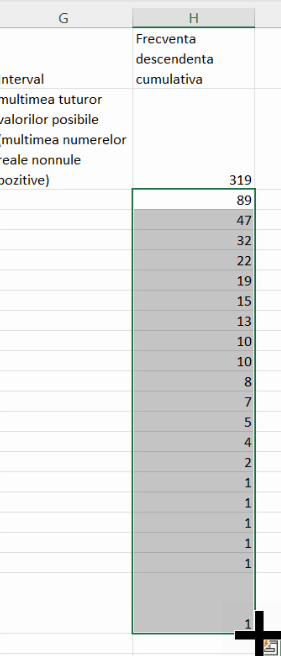
Descrierile acestor frecvențe vin din ceea ce ele prezintă:
- 89 este frecvența submulțimii după eliminarea, din setul tuturor valorilor posibile, a grupei “de la 1 la 20000”, deci este frecvența submulțimii de localități cu populație peste 20000
- 47 este frecvența submulțimii după eliminarea, din setul “peste 20000”, a grupei “de la 20001 la 40000”, deci este frecvența submulțimii de localități cu populație peste 40000
- etc
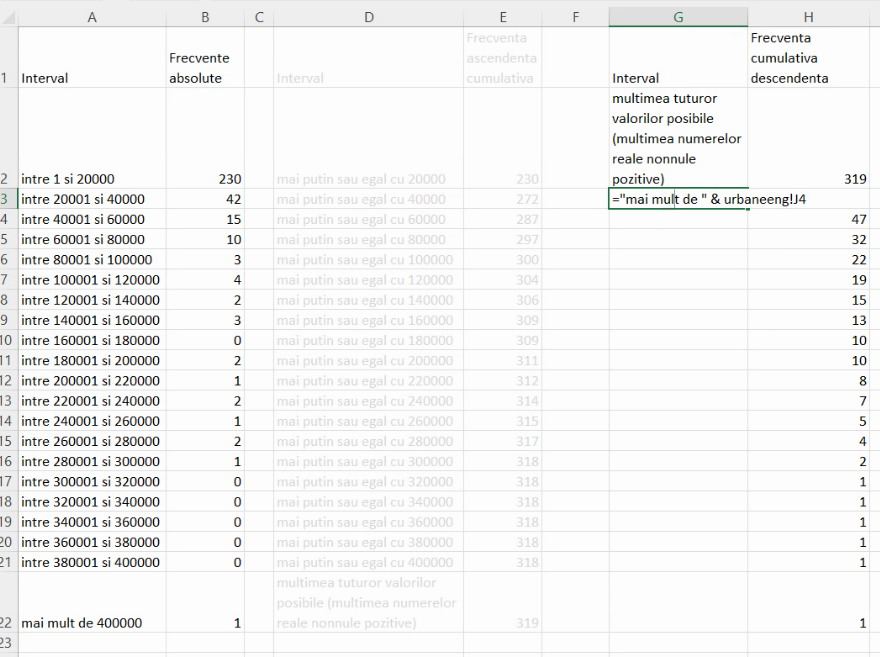
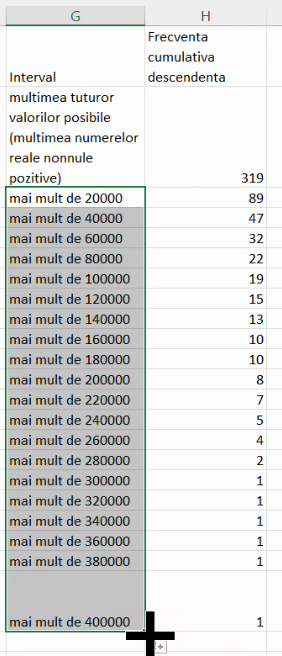
Imagine de mai sus reprezintă tabelul frecvențelor cumulative descendente, scris în convenția economiștilor, adică fără mulțimea vidă, dar cu mulțimea tuturor valorilor posibile.
Pentru a obțineun tabel similar cu cele din problemele din culegeri, este necesar doar să alipim cele trei tabele deja existente:
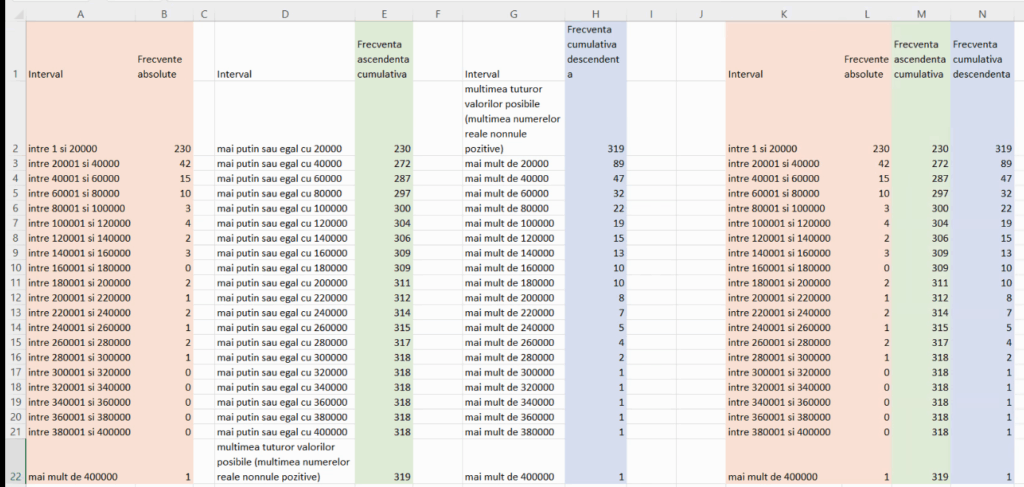
Interpretarea celor două coloane din tabelul criptic este:
- Pentru frecvențe cumulative ascendente, va fi vorba de cel mai îngust interval de la limita inferioară a valorilor posibile (-∞ în exemplul din capitolul precedent, 0 aici), care cuprinde și intervalul de pe coloana etichetelor. De exemplu, 272 din dreptul lui “între 20001 și 40000” se referă la cel mai îngust dintre “mai puțin sau egal cu 20000” (aici (0,20000]), “mai puțin sau egal 40000” (aici (0,40000]) etc, care include și “între 20001 și 40000”. Este vorba, desigur, de (0, 40000].
- Pentru frecvențe cumulative descendente, va fi vorba de cel mai îngust interval de la limita superioară a valorilor posibile (+∞ în exemplul din capitolul precedent și aici), care cuprinde și intervalul de pe coloana etichetelor. De exemplu, 89 din dreptul lui “între 20001 și 40000” se referă la cel mai îngust dintre “mai puțin de 20000” (aici (20000, +∞)), “mai puțin de 40000” (aici (40000, +∞)) etc, care include și “între 20001 și 40000”. Acest 89 corespunde deci lui (40000, +∞).
Pentru frecvențele relative, fie ele de grupă-interval sau cumulative, este suficient să împărțiți toate frecvențele absolute la efectivul colectivității, care poate este deja în tabel, ca cea mai mare frecvență ascendentă și cea mai mare frecvența descendentă:
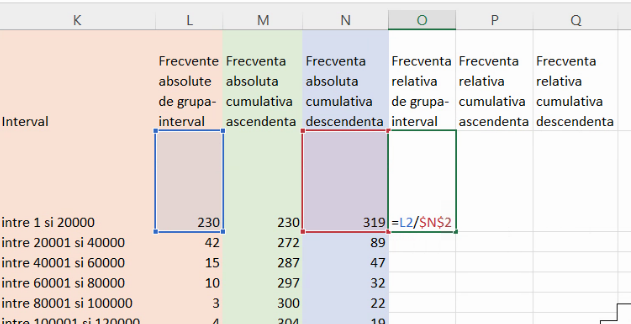
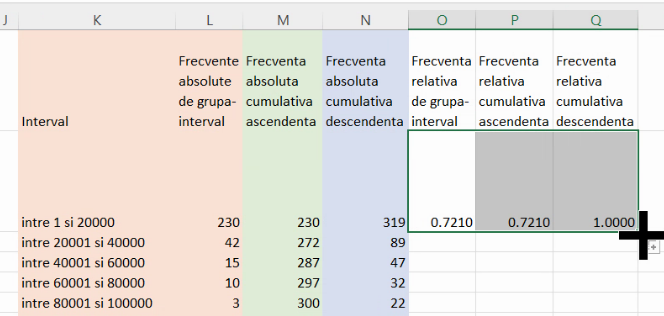
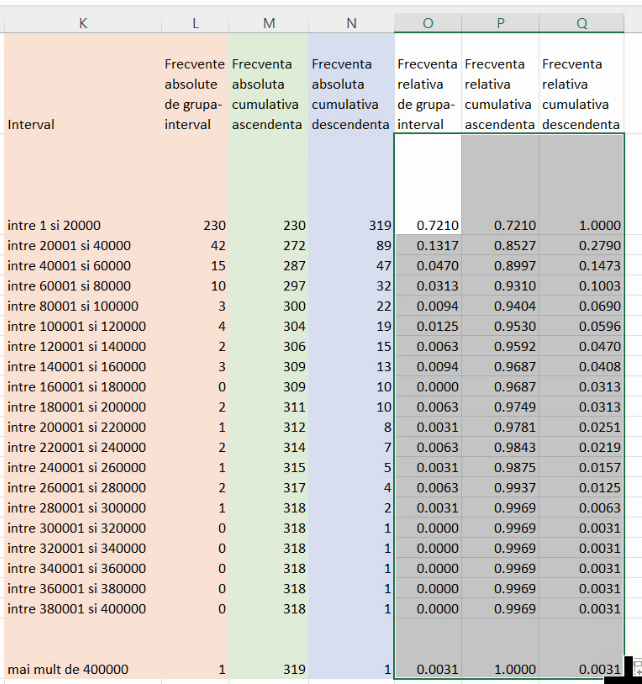
Rezultatul acestor calcule este prezentat în fișierul acesta.
Grupare pe intervale cu PivotTable
Vom începe cu un fișier în care am obținut o coloană cantitativă, numerică, a populației fiecărei localități urbane din România, în manieră agnostică față de setările computerului. Vom selecta datele, acționa butonul PivotTable și alege Foaie nouă. În noul PivotTable, vom cere ca liniile să fie definite de valori ale efectivului populației, iar valorile din tabel să fie calculate cu Count.
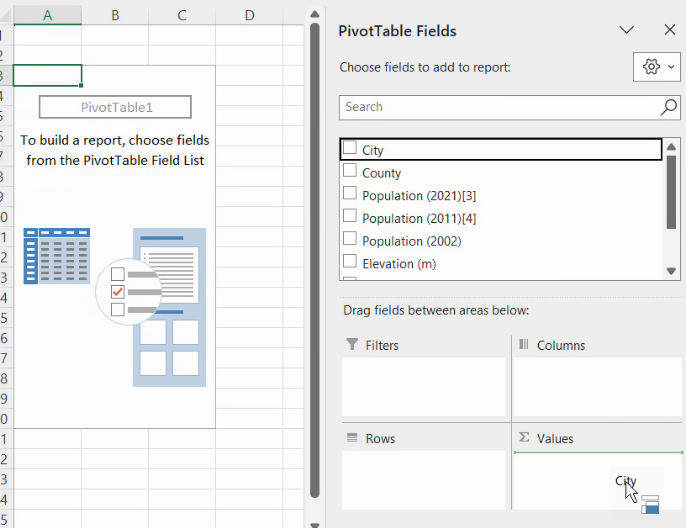
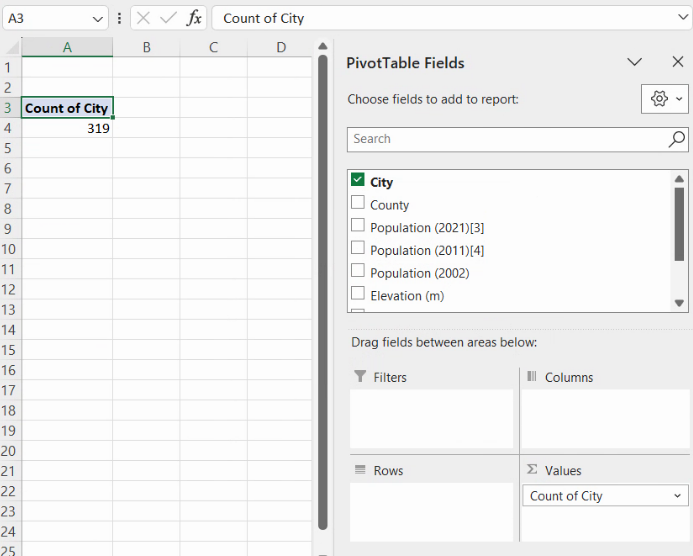
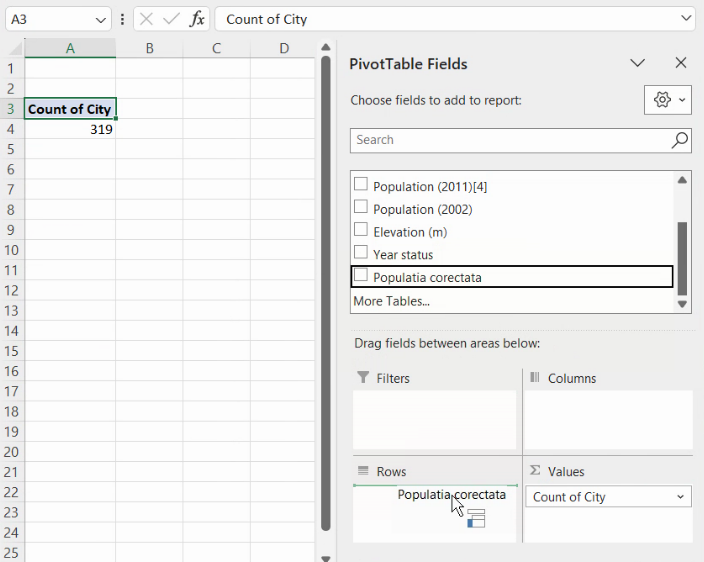
Tabelul astfel generat arată distribuția pe valori individuale:
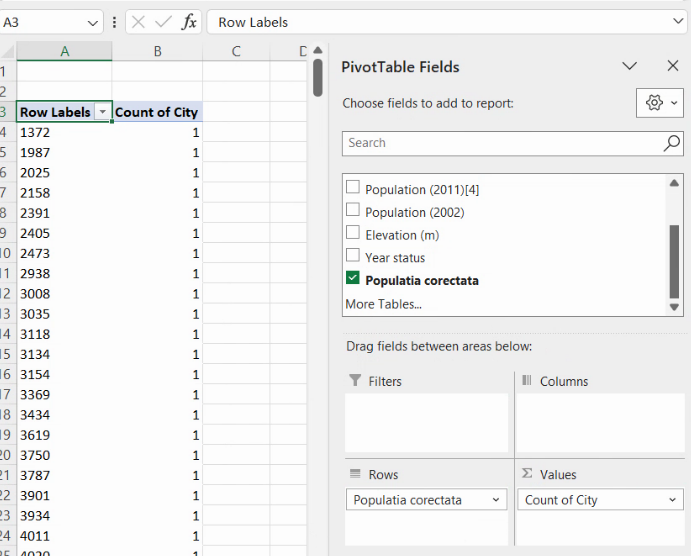
Un clic dreapta pe oricare din valorile caracteristice va produce un meniu:
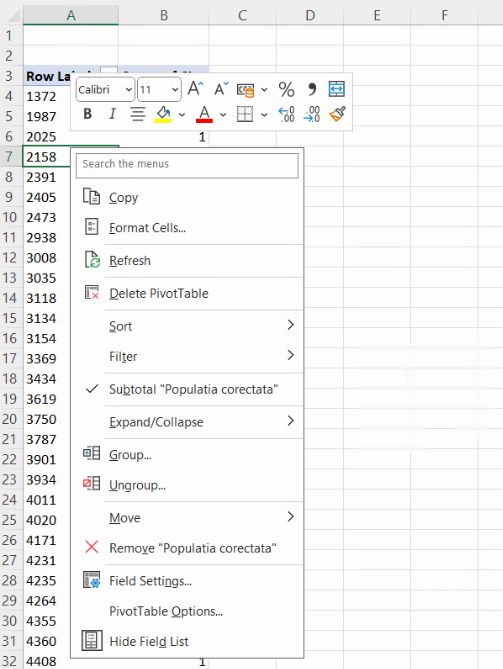
Alegerea opțiunii Group va aduce ]n prim plan acest dialog:
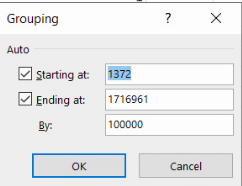
Pentru a replica intervalele de mai sus, setăm limitele 0 și 400000, precum și lățimea de interval de 20000:
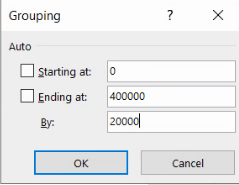
Aplicăm setarea cu OK, obținând
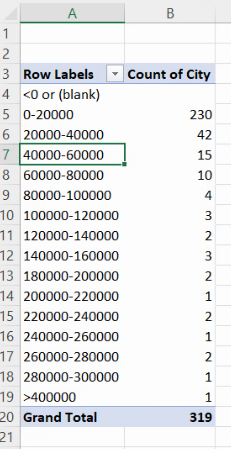
Limitele intervalelor se suprapun aparent, însă în realitate intervalele sunt închise numai la limita inferioară (invers față de FREQUENCY()).
Rezultatele acestor calcule sunt prezentate aici.
Reprezentări grafice ale seriilor de distribuție pe intervale
Vom începe cu același fișier ca în secțiunea precedentă. Coloana H ar trebui să cuprindă valori numerice:

Histograma cea mai elocventă pentru majoritatea cazurilor este cea construită automat de Excel. Selectăm coloana cu valori, și alegem Insert- Chart – Histogram
Însă în acest caz, histograma va fi deformată de diferența enormă dintre efectivul Bucureștiului și celelalte:
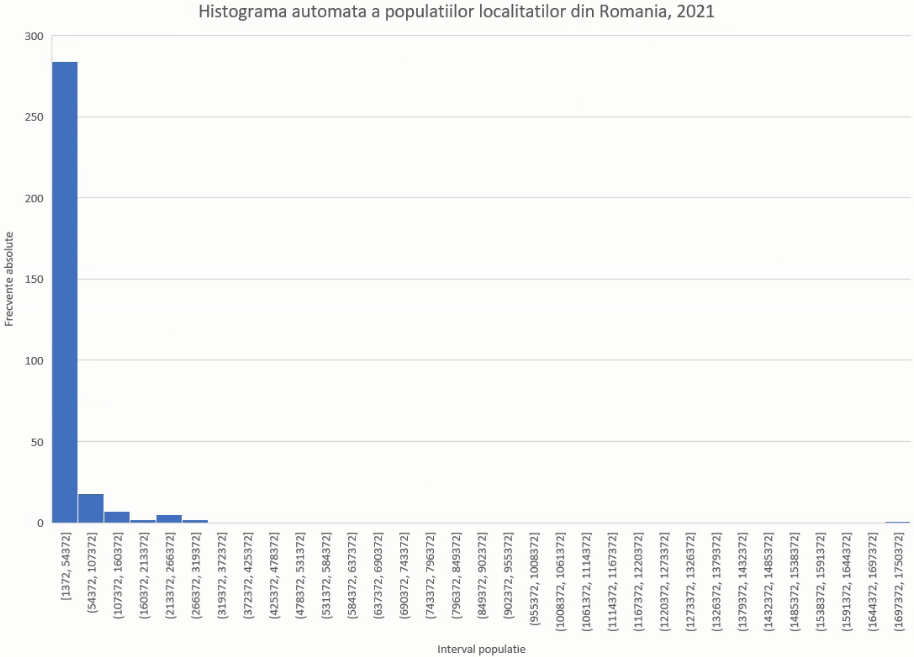
Un alt motiv pentru care nu putem folosi metoda automată este că limitele de interval sunt numere ne-rotunjite, ba chiar cu zecimale, ceea ce va îngreuna lectura. Vom construi manual histograma cu frecvențele redate de FREQUENCY():
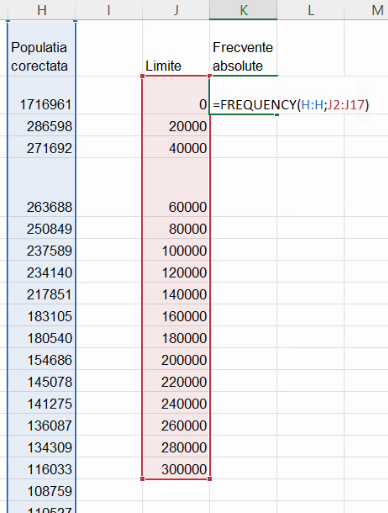

Excel nu permite construirea manuală de histograme corecte, pentru că nu permite etichete între coloane, ci numai la mijlocul fiecărei coloane. Pentru etichetele de coloană putem crea ca în secțiunea similară precedentă, “cel mult 0”, “între 1 și 20000”, “între 20001 și 40000″ …”între 280001 și 30000”, și “mai mult de 300000”:
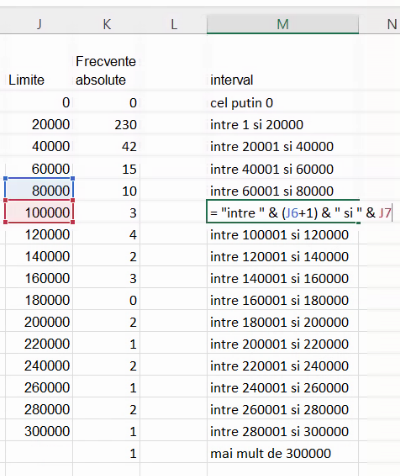
Copiem frecvențele în coloana următoare:
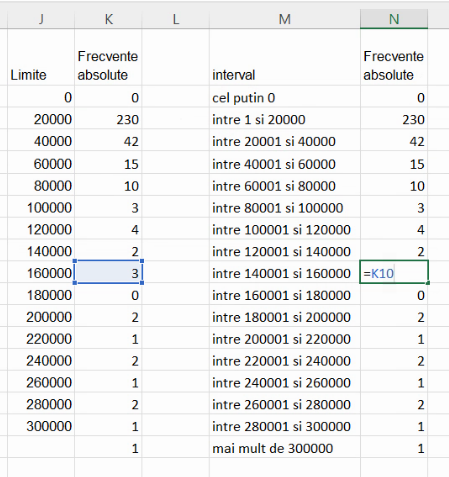
Selectăm tabelul M1:N19, și alegem Insert – Chart – 2D column – Clustered column (primul buton):
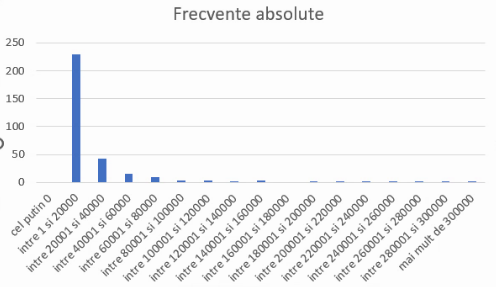
Graficul obținut mai necesită doar titluri de axă și anularea spațiului dintre coloane, cel din urmă cu Format – Data Series
Ci click dreapta pe suprafața graficului nealocată vreunuie elemnet al să obținem un meniu, din care putem alege să mutăm graficul pe altă foaie de calculȘ
Rezultatul este un grafic de distribuție mai corect pentru o serie homogradă, și, involuntar, o demonstrație a unei metode numite “prelucrarea intervalelor nemărginite” (“treatment of open-ended classes”). De cel mai multe ori, statisticianului îi parvin numai date la nivel de grupă, ca cele produse de FREQUENCY(), incluzând intervale nemărginite.
- În acest exemplu, am putea ști că populația localităților din România este maxim 2 milioane, și am putea reformula “mai mult de 300 de mii” ca (300000, 2000000).
- De regulă, nu cunoaștem astfel de detalii, așa că va trebui să presupunem. În lipsa altor informații, cea mai bună presupunere pentru lățimea intervalului nemărginit va fi lățimea intervalului adiacent. Aici, “mai mult de 300 de mii” a primit lățimea intervalului adiacent, (280000, 300000), și este deci aproximat de Excel cu (300000, 320000).
Similar, lățimea lui “cel mult 0” a fost aproximată cu lățimea lui (0,20000), și deci a devenit (-20000,0).
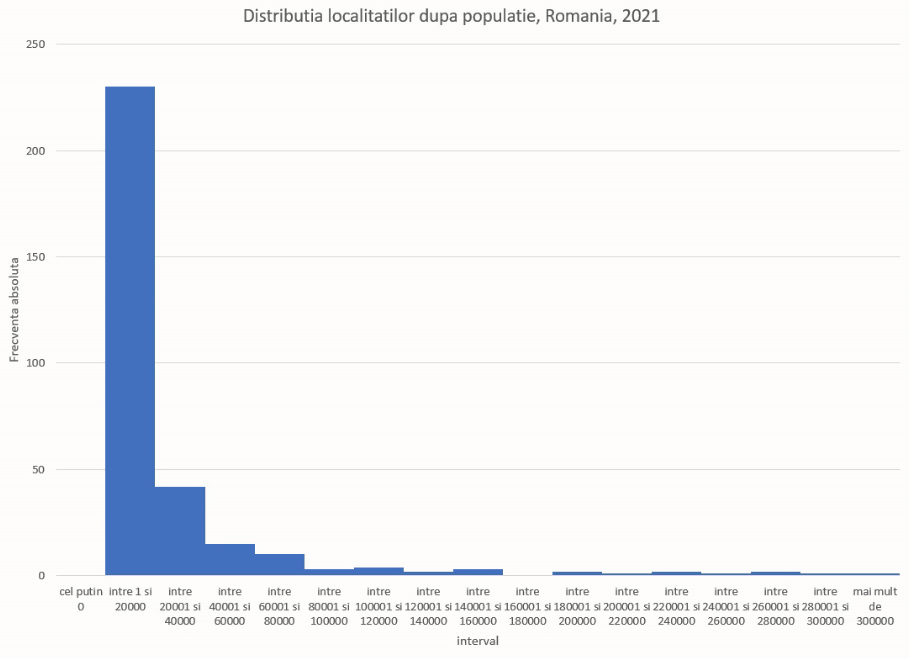
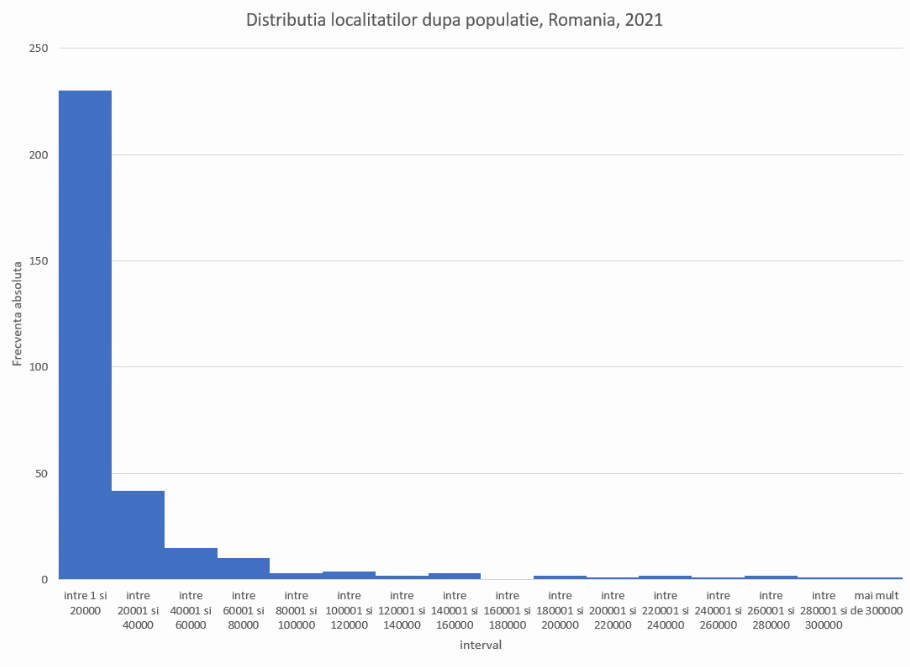
Întrucât numerele a căror distribuție este reprezentată aici nu pot fi negative, putem elimina din tabelul de distribuție primul interval (“cel mult 0”):
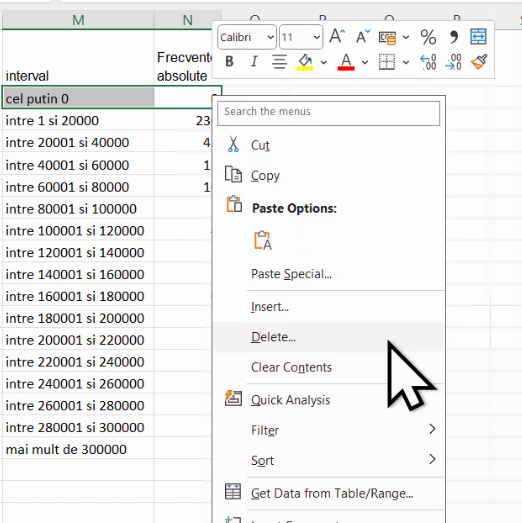
Rezultatul se va reflecta în graficul de distribuție, prin eliminarea coloanei inutile:
Pentru poligonul frecvențelor, va trebui să fixăm pozițiile fiecărui element atât ca ordonată (folosind tot frecvența absolută), cât și ca abscisă. Pentru cea din urmă va fi necesar mijlocul de interval (eng. class midpoint). Vom construi tabelul necesar noului grafic, prin repetarea tabelul din regiunea M:N în regiunea P:Q, cu modificarea primei coloane:
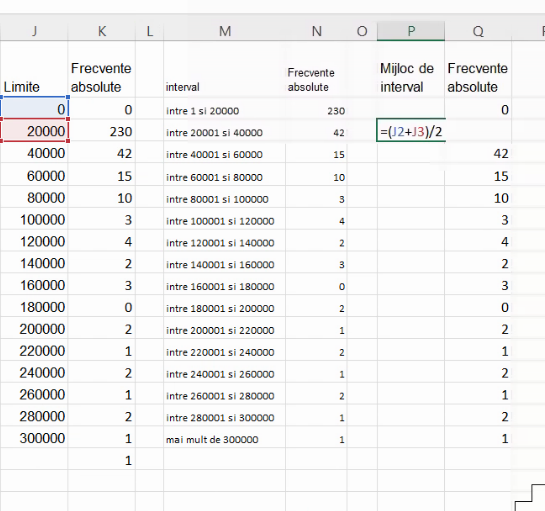
Cu n limite, putem calcula doar n-1 poziții de mijloc de interval:
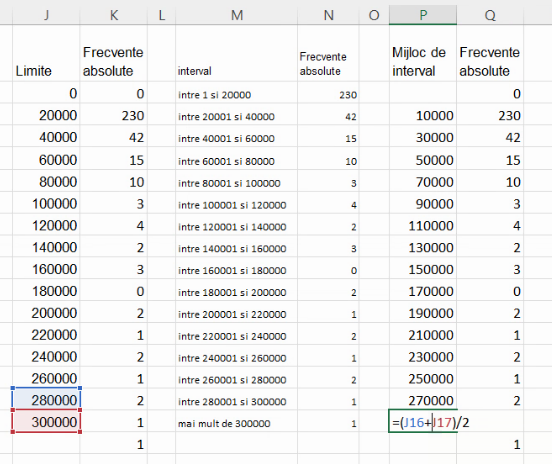
Pentru intervalele extreme, va trebui să folosim aproximăm mijlocul de interval cu o metodă similară cele de aproximare a lățimilor. Dacă lățimea lui “mai mare de 300 000” este aproximată cu lățimea lui (280000, 300000], și distanța de la marginea la centrul lui “mai mare de 300 000” trebuie aproximată cu distanța de la marginea la centrul lui (280000, 300000].
În imaginea de mai jos, centrul intervalului (280000, 300000], adică 290 000, apare cu chenar roșu. Deci distanța de la margine la centru pentru (280000, 300000] este la fel de bine calculată ca
- distanță de la numărul din celula roșu (290000) către cea albastră (marginea superioară, 300000)
- distanță de la numărul din celula roșu (290000) către cea violetă (marginea inferioară, 280000).
Alegând-o pe a doua, vom scrie:
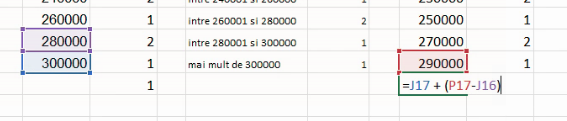
Similar, mijlocul primului interval, “cel mult 0”, va fi calculat prin scădere de la limita sa superioară (0) a unei distanțe de la centru la margine din intervalul adiacent (aici, din (0,20000)):

Am obținut un set complet de perechi de numere pe care le dori ca repere ale poligonului frecvențelor:
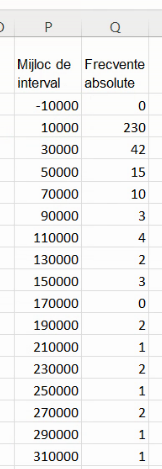
Pentru a marca pe un grafic toate aceste puncte de coordonate (-10000,0), (10000, 230) etc, vom crea o corelograma (scatterplot). Pentru a obține și linia care le unește, vom selecta tabelul de date și vom alege Insert – Chart – Scatterplot – Scatter with straight line and markers (al patrulea buton de sub scatter):
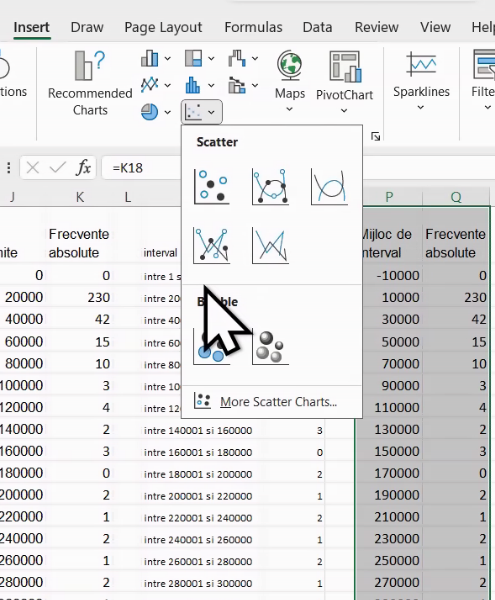
Rezultatul va fi un poligon al frecvențelor cu mici deficiențe de finisaj:
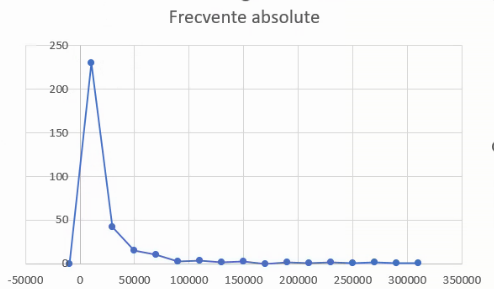
Mutăm graficul în altă foaie, adăugăm titluri la axe, actualizăm titlul graficului:
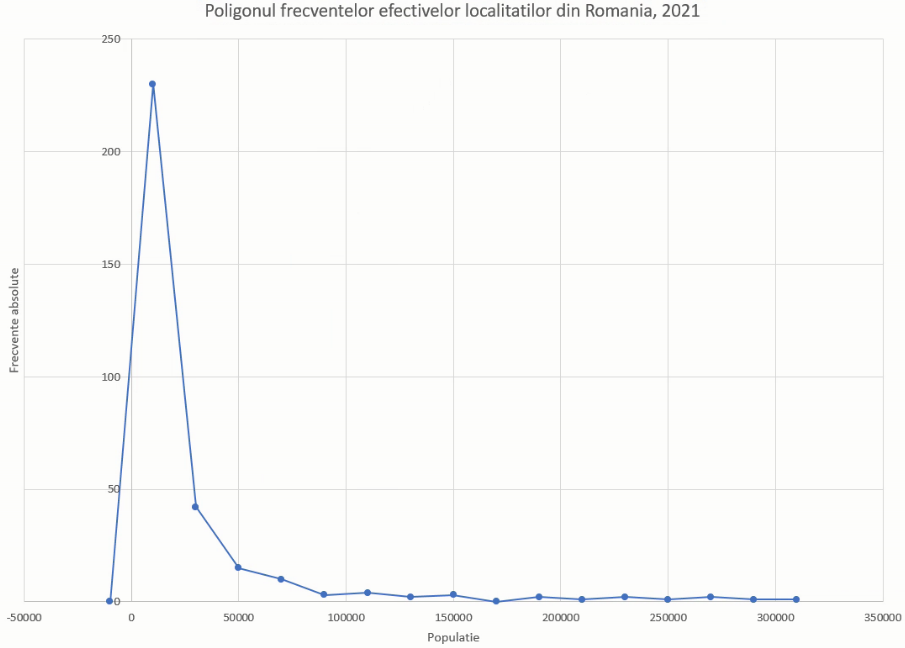
Un poligon al frecvențelor este adus la zero la valoarea minim și maximă a variabilei analizate. La limita inferioară, minimul posibil este 0, motiv pentru care ar trebui să introducem un punct la (0,0). Faptul că (0,0) este limita de la stânga acestuia implică necesitatea ștergerii punctului cu x=-10000, obținând:
Graficul va fi automat actualizat:
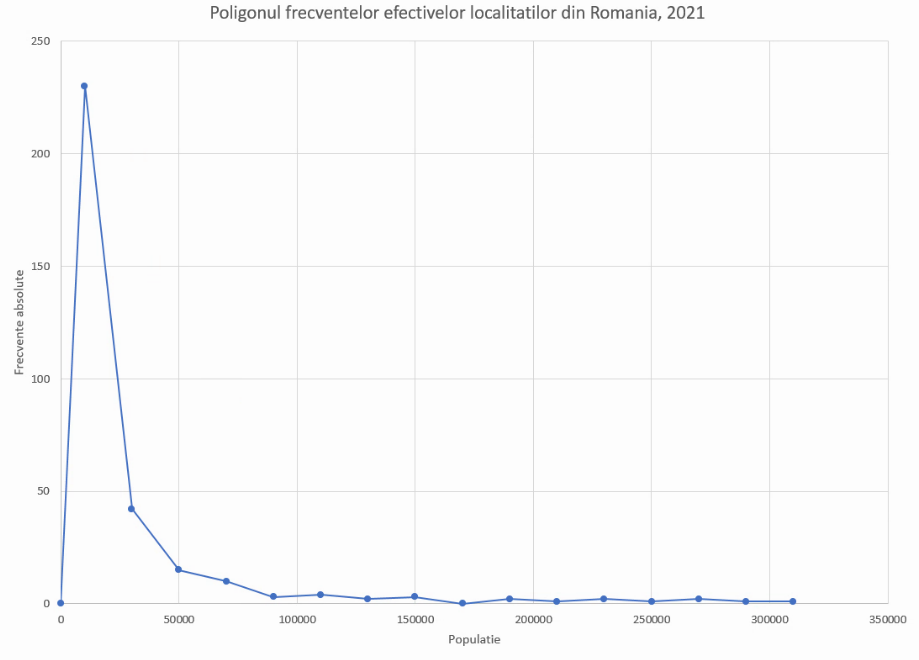
Pentru maximul posibil al lui X, valoarea cea mai potrivită este +∞, însă aceasta nu poate fi reprezentată pe un grafic. De asemenea, pentru experții în geografia populației, mai există varianta max(X) ≈ 2000000 (populația Bucureștiului). Pentru situațiile în care maximul posibil nu este cunoscut, vom aplica același principiu ca până aici: lățimea unui interval semimărginit va fi aproximată cu lățimea intervalului adiacent (aici (280000, 300000)). Vom atașa un punct la baza tabelului de coordonate:
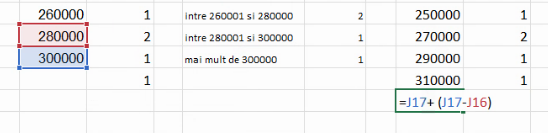
Excel nu va sesiza adăugirea. Va fi nevoie de extinderea manuală a graficului. Click dreapta pe zone ale graficului ce nu conțin elemente și alegeți Select Data:
De regulă, va fi suficientă editarea lui Chart data range, pentru a scrie Q19, în loc de Q18:
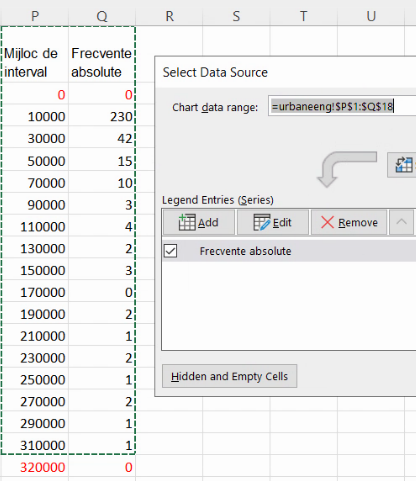
Nu folosiți taste cu săgeți la editarea adreselor. Ștergeți “8” și scrieți “9” în locul lui:
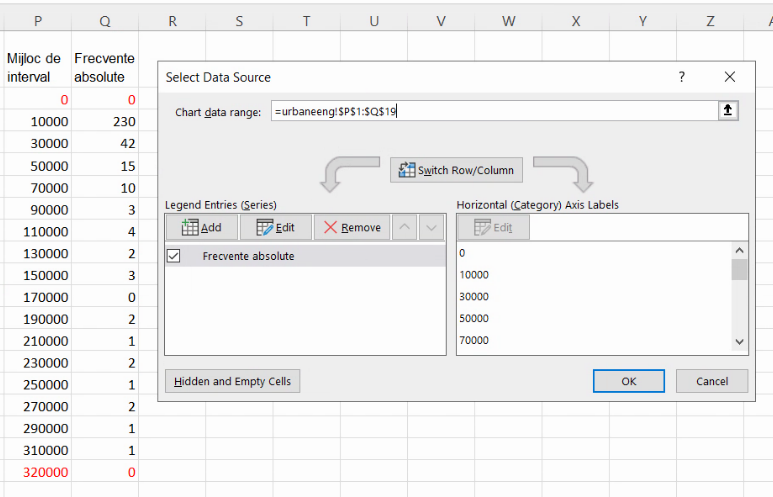
Acesta este poligonul frecvențelor:
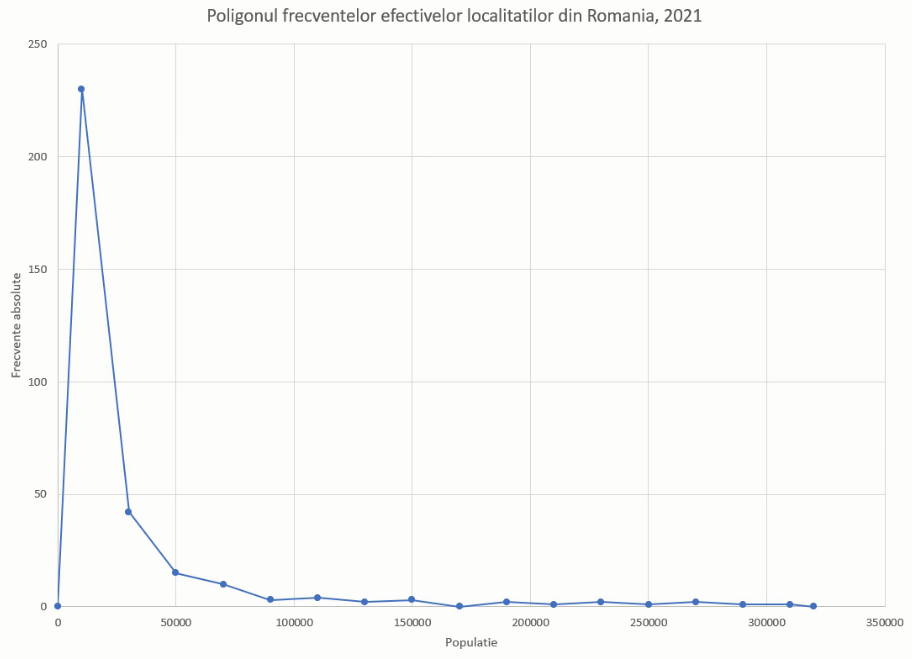
Pentru curba distribuțiilor cumulative ascendente putem începe cu tabelul ce le descrie literal. Pentru n limite, vom avea n intervale de frecvență cumulativă ascendentă. În situația în care limita inferioară era -∞ aceste intervale se descriu ca “mai puțin de X” sau “cel mult X”, în funcție de închiderea / deschiderea intervalului. La acestea se adaugă mulțimea vidă și mulțimea care cuprinde toate valorile posibile (mulțimea numerelor reale, dacă valorile posibile se întind de la -∞ la +∞):
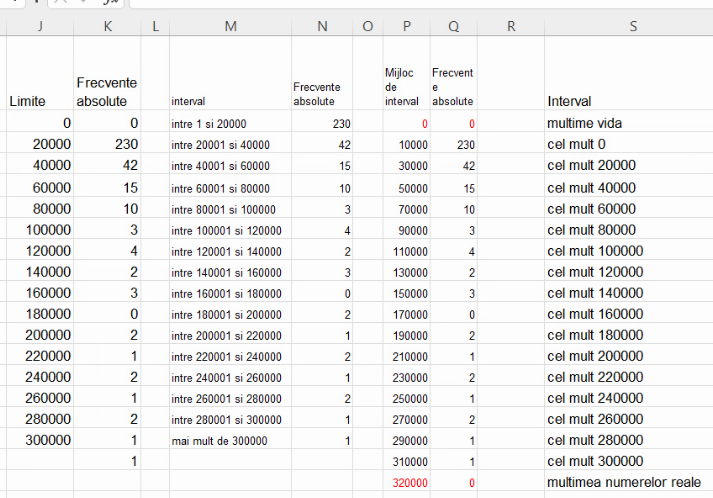
Pentru situația în care limita inferioară este 0 în loc de -∞, avem tot n intervale, o mulțime vidă, și o mulțime care acoperă toate variantele:
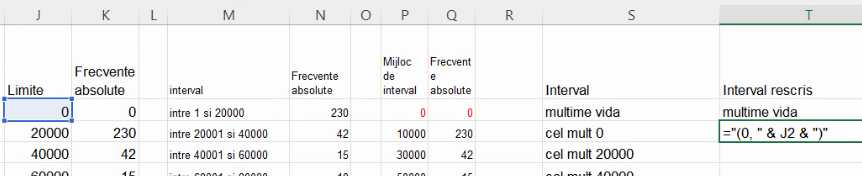
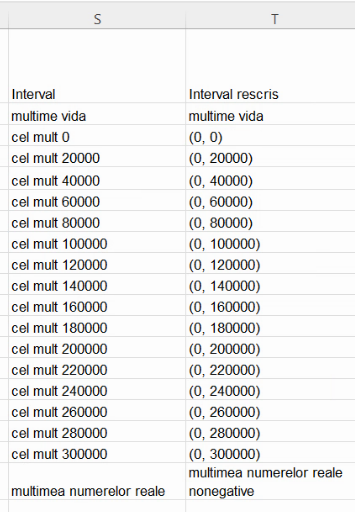
În ambele cazuri, începem șirul frecvențelor cumulative ascendente cu zero (frecvența absolută a mulțimii vide), după care calculăm cu adunări consecutive la frecvența cumulativă ascendentă imediat precedentă:
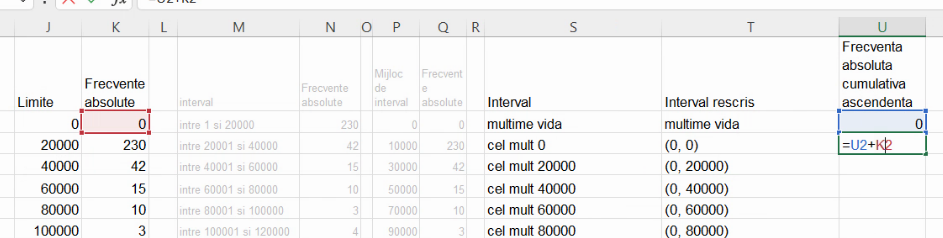
De exemplu, frecvența absolută a lui “cel mult 140000” este suma frecvențelor lui “cel mult 120000” și “între 120001 și 140000”:
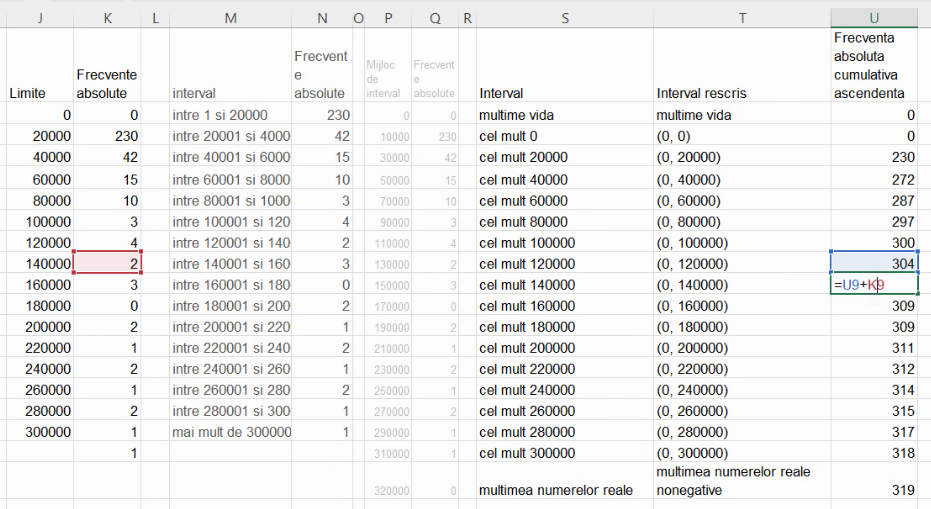
Pentru o curbă a frecvențelor cumulative ascendente, vom crea perechi de coordonate de forma (margine superioară a intervalului, frecvență cumulativă până la acea limită):
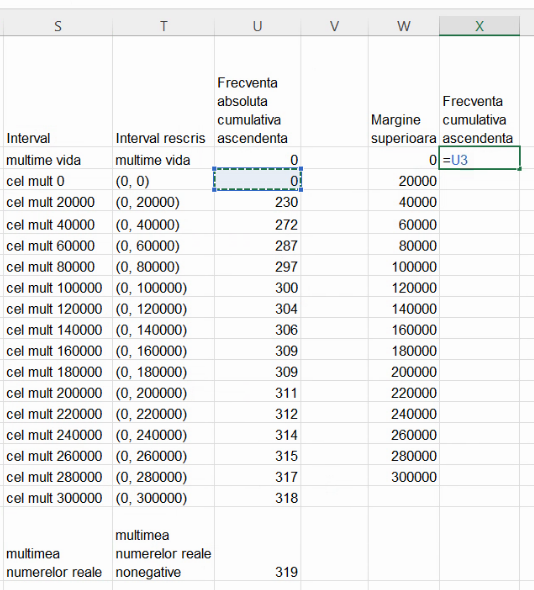
Evident, vom omite mulțimea vidă și mulțimea fără limită superioară. Pentru reprezentare grafică, selectăm acest nou tabel și folosim din nou Insert – Chart – Scatterplot – Scatter with straight line and markers (al patrulea buton de sub scatter):

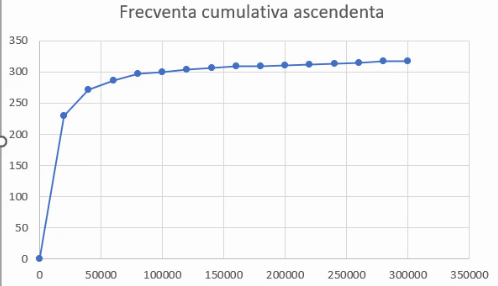
Rezultatul de mai sus necesită aceleași cosmetizări:
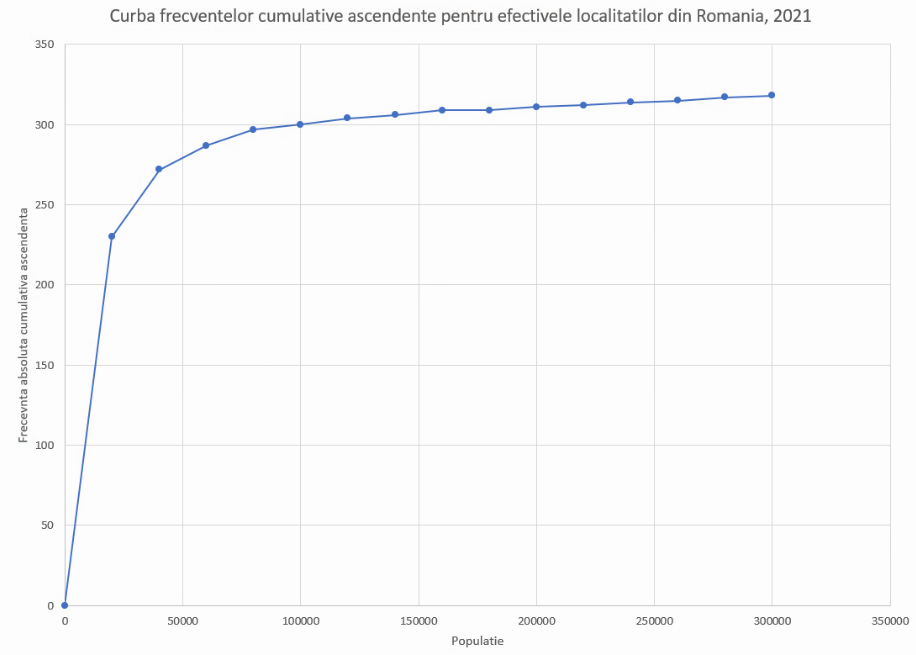
Dacă ați forțat prezența lui -∞ și -∞, respectiv al mulțimii vide și a mulțimii numerelor reale, și dacă limitele au fost alese de așa natură încât cele două intervale extreme (aici, “cel mult 0” și “cel puțin 30000”) să aibă efective zero, primul și ultimul punct de pe curba frecvențelor cumulative ascendente se vor afla în locul unde trebuie să se afle, la y=0 și respectiv y=N (efectivul colectivității).
În exemplu nostru, primul punct are y=0, însă ultimul nu se află la y=N. Vom mai adăuga un punct la y=N, cu x la valoarea maximă posibilă a variabilei discutate.
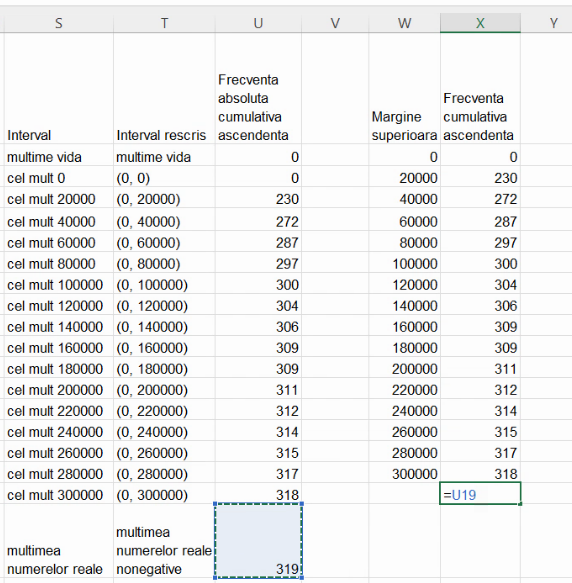
Așa cum am menționat mai sus, există mai multe opțiuni, dar în acest exemplu vom presupune un interval final de lățime egală cu cel adiacent lui.


Noul punct nu va fi adăugat automat la curba frecvențelor cumulative ascendente, așa că vom extinde manual cu Select data, ca mai sus:

Trecerea de la W17 la W18 produce curba completă a frecvențelor cumulative ascendente:
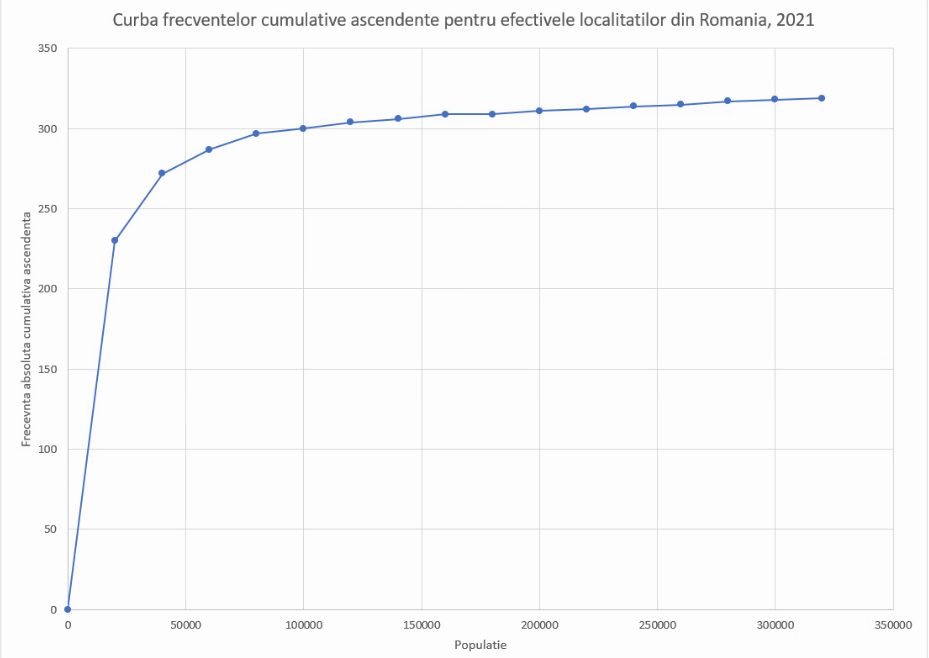
Pentru curba frecvențelor cumulative descendente, vom proceda similar, construind un tabel lizibil cu cele n intervale limitate, cu mulțimea vidă și cu mulțimea numerelor reale. Aici, calculul frecvențelor cumulative descendente începe de la efectivul colectivității și se calculează cu scăderi consecutive:
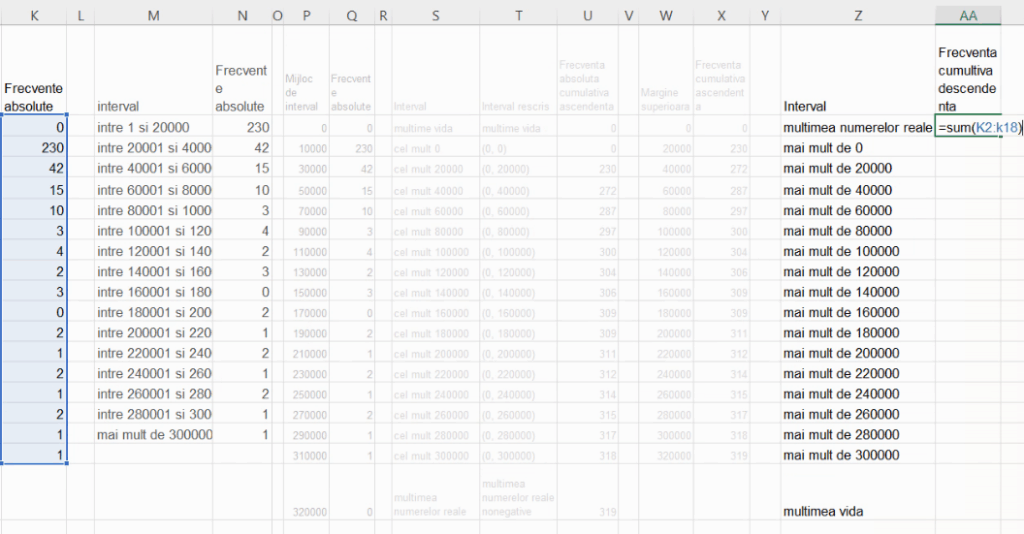
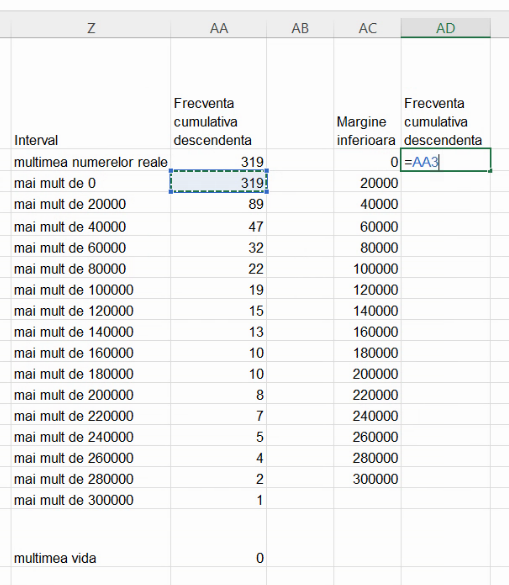
Vom construi tabelul ajutător, cu coordonate de forma (margine inferioară, frecvență cumulativă descendentă):
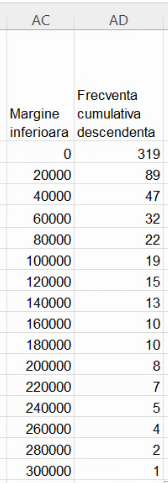
Această serie de frecvențe cumulative are aceeași deficiență ca cea precedentă, fiindcă nu se întinde de la y=N (efectivul colectivității) la y=0. Deși frecvența cumulativă descendentă maximă atinge efectivul colectivității, y=0 nu este atins. Vom introduce un punct de coordonate y=0, al cărui x este, din nou, valoarea maximă posibilă a variabilei analizate. Din nou, vom evita -∞ și 2 milioane, folosind aproximarea tipică pentru intervale nemărginite, lațimea acestuia fiind aproximată cu lățimea intervalului adiacent:
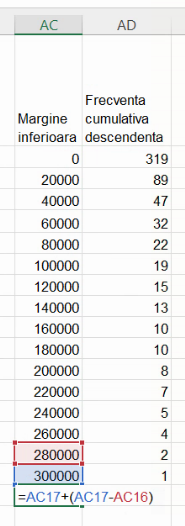
Selectăm celulele din cel mai recent table, și alegem Insert – Chart – Scatterplot – Scatter with straight line and markers. Cosmetizam ca mai sus:
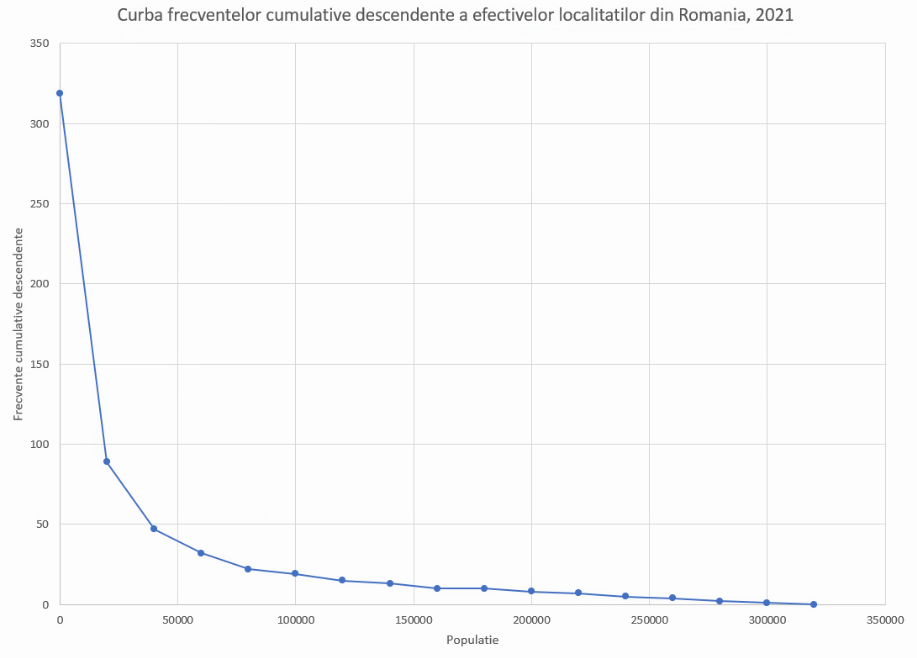
Pentru graficul ogiva, începem prin a repeta graficul frecvențelor cumulative ascendente. Selectăm tabelul cu coordonatele lor, folosim Insert – Chart – Scatterplot – Scatter with straight line and markers:
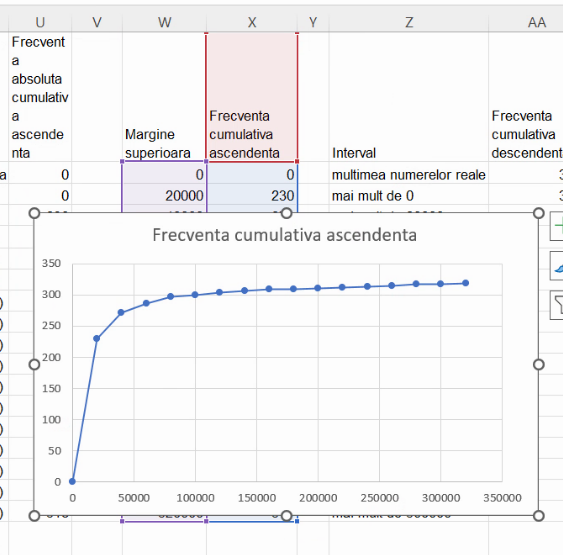
Activăm Select Data:
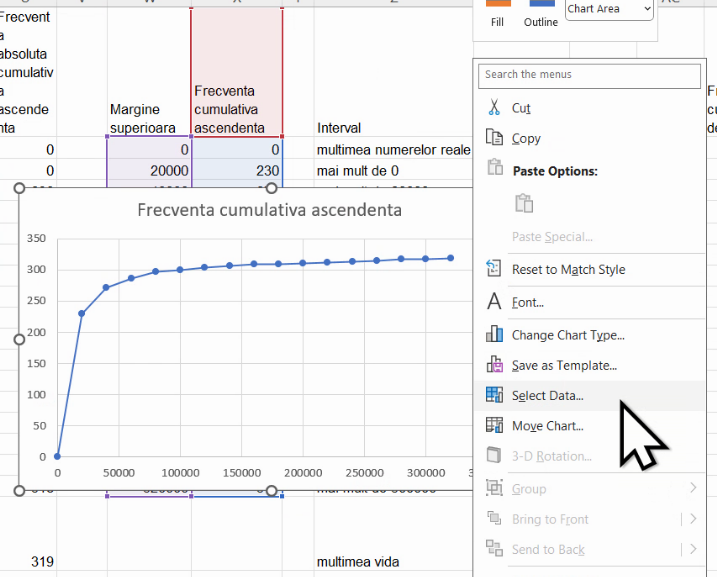
Pentru a adăuga o nouă serie bidimensională, folosim Add de deasupra listei de Series:
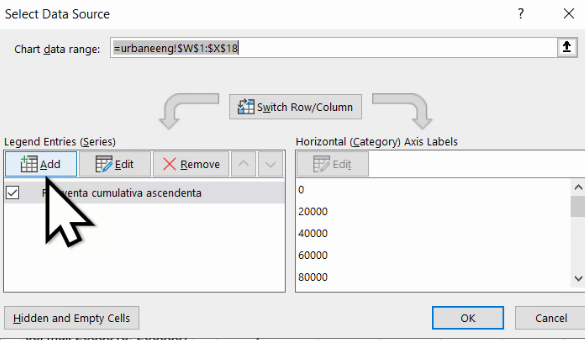
În noul dialog, cele trei butoane de formă similară vă permit selecția cu mausul:
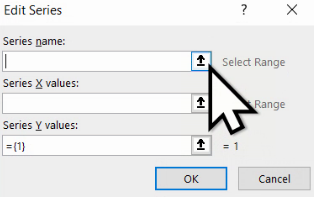
Acționăm pe primul pentru a selecta numele noii serii:
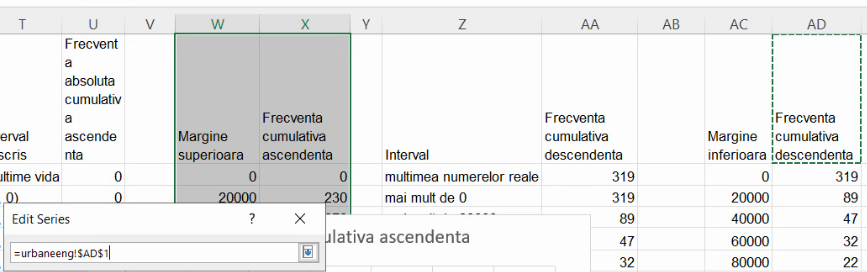
Pentru a indica Excel că am finalizat selecția, acționăm butonul de lângă adrese:
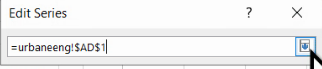
Repetăm selecția pentru valorile lui X din coloana AC:
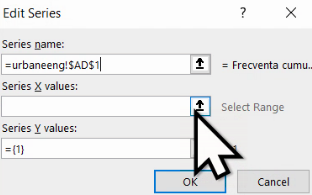
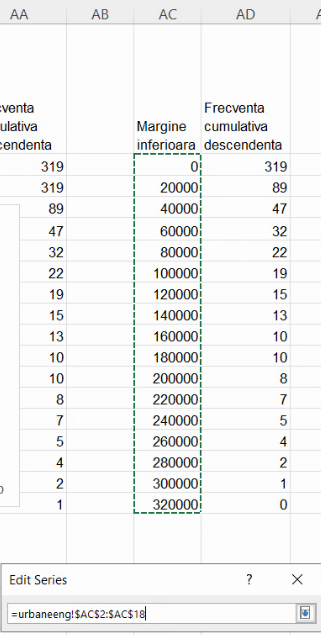
Înainte de a repeta procesul pentru selecția Y-urilor, trebuie eliminată valoarea deja existentă, “={1}”.

Dați clic la marginea ei dreaptă, și folosiți tasta Backspace; sau dați clic la marginea ei stângă și folosiți tasta Delete. Nu folosiți taste săgeată sau mausul până ați golit cutia de conținutul ei vechi:
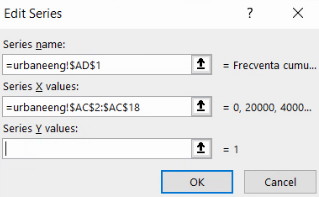
Acum puteți indica cu selecție cu maus, că valorile lui Y vor veni din coloana AD:
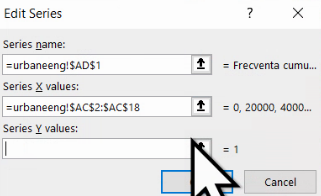

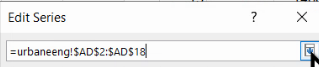
Dacă aveți situația de mai jos, ați terminat de definit noua serie:
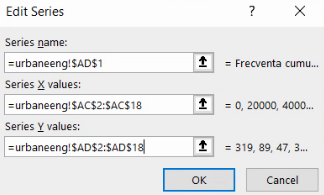
Cu două clicuri pe butoane OK, reveniți la contextul general, producând un grafic ogivă necosmetizat:
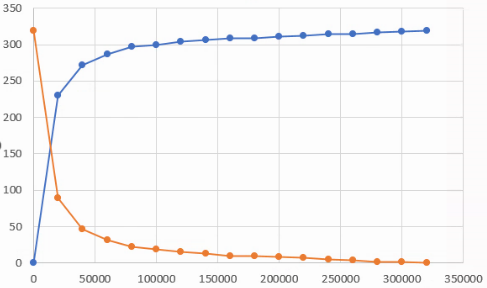
Adăugăm titluri:
Mai este necesar un element vital aici. Fără legendă, nu va fi clar ce reprezintă cele două culori. Ca orice alt element lipsă, legenda va fi adăugată din Chart design – Add chart element:
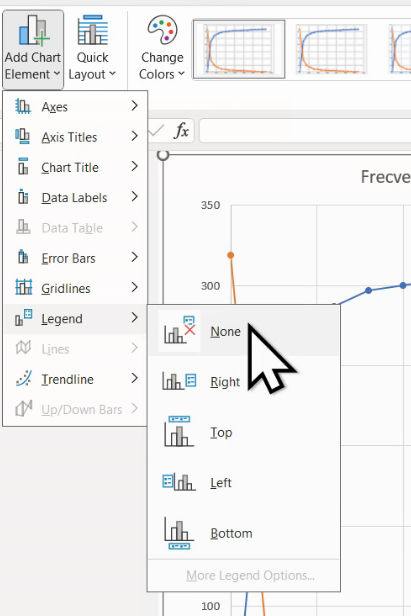
Rezultatul este un grafic ogivă clar:
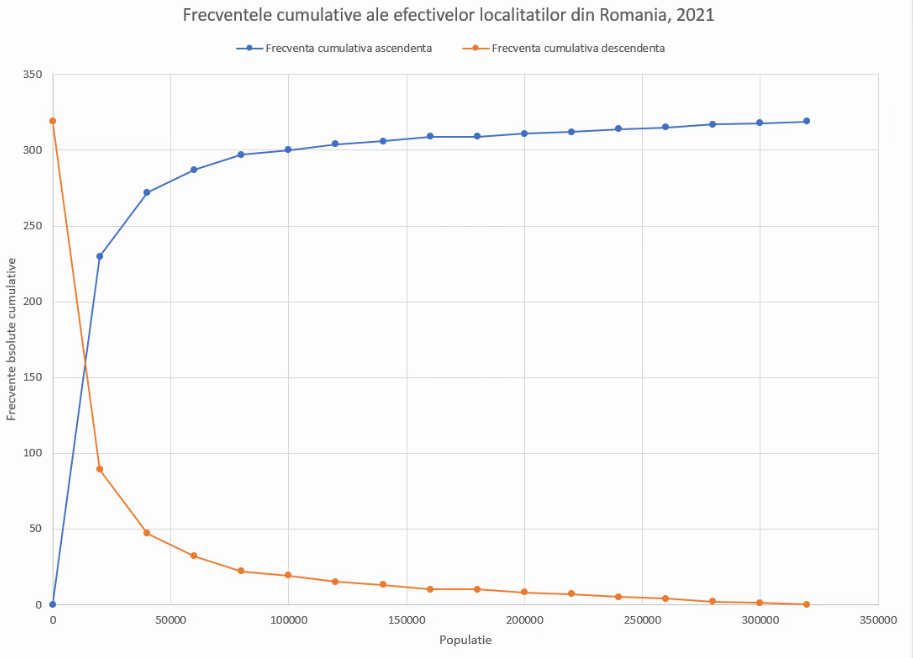
Un fișier cu aceste procesări se găsește aici.
